The Project Gutenberg eBook of The Aneroid Barometer: Its Instruction and Use, by George Washington Plympton
Title: The Aneroid Barometer: Its Instruction and Use
Author: George Washington Plympton
Release Date: December 9, 2022 [eBook #69513]
Language: English
Produced by: deaurider and the Online Distributed Proofreading Team at https://www.pgdp.net (This file was produced from images generously made available by The Internet Archive)

THIRD EDITION.
REVISED AND ENLARGED.
NEW YORK:
D. VAN NOSTRAND COMPANY,
23 Murray and 27 Warren Street.
1890.
Copyright, 1884,
By D. VAN NOSTRAND.
| Page. | |
| Chapter I.—The Atmosphere | 5 |
| Chapter II.—Barometric Measurements of Altitudes | 27 |
| Chapter III.—Aneroid Barometers: Their Construction | 39 |
| Chapter IV.—The Use of Aneroid Barometers | 52 |
| Chapter V.—Suggestions in Regard to the Selection and Systematic Use of an Aneroid | 77 |
| Table I.—Prof. Airy’s Table of Altitudes | 88 |
| Table II.—Logarithmic Table | 106 |
| Table III.—Metric Altitude Table | 121 |
| Table IV.—Corrections for Mercurial Barometer | 125 |
| Table V.—Boiling Point of Water corresponding to Different Barometric Pressures | 126 |
The fact that the first edition of this little manual is entirely exhausted is a sufficient indication that it supplied a want. As the use of the Aneroid Barometer is on the increase, the presumption is that there will be a further demand for this book of tables and instructions.
It has been thought advisable to rearrange the matter and to increase it by fuller descriptions of different instruments; and what is of more importance to the novice in measuring altitudes, to add a number of examples.
Another table has also been added to the collection of the previous edition.
[Pg 5]
THE ANEROID BAROMETER:
ITS CONSTRUCTION AND USE.
The gaseous envelope which surrounds our globe, and to which we give the name of atmosphere, is subject to many and varied changes. In the relative amount of the two gases which chiefly compose it, it remains marvelously constant; yielding upon analysis the same ratio of oxygen to nitrogen for all latitudes and all altitudes. It is only within a few restricted and generally confined areas where the natural chemical processes of respiration, combustion or fermentation are active, that the free oxygen is found to be notably deficient, and the product, [Pg 6] carbonic dioxide, which exists normally to the extent of one twenty-fifth of one per cent., is, to a corresponding extent, in excess.
When, however, we regard the conditions which arise from its physical properties, no such constancy is observable. Indeed, it seems the most fitting type of a transitory state, and whether we regard the temperature, the moisture, the pressure resulting from its weight, or the direction and velocity of its motions, we can only acquaint ourselves with the limits within which these conditions have been known to vary. The nature of the changes within these limits we cannot, in the present state of our knowledge, assume to predict for the future, except for very limited periods; and even then the prediction is set forth only as a “probability.”
Certain average conditions are noticeable as belonging to certain areas or zones of the earth, and differing somewhat among themselves, especially as to greater or less range in temperature, moisture, etc. To such general conditions we apply the term climate. [Pg 7]
The department of science which regards the physical phenomena arising from these varying conditions is called meteorology. The instruments employed with which to indicate or measure the extent of these changes, are of various kinds. Thus the thermometer indicates the relative temperature, the hygrometer the humidity, the anemometer the force or the velocity of the wind, and the barometer the pressure of the air which arises directly from its weight.
It is with the last of these instruments that we are especially concerned in the present essay. It has two quite distinct uses: One to indicate the varying pressures of the air at some fixed point for meteorological purposes, and the other to indicate difference in altitude of points to which the instrument is carried by affording a measure of the greater or less amount of atmosphere above it. Before using the instrument to measure altitudes it is important to become somewhat familiar with its use as a stationary instrument. The [Pg 8] barometer most frequently employed for such use is the one invented by Toricelli in 1643. It is too well known to require description here. It will be sufficient to say that it measures the varying pressure of the air by the varying length of a column of mercury which balances the pressure.
When the barometer is employed for the purposes of meteorology only, the following facts are taken into consideration. We quote from Buchan’s “Handy Book of Meteorology.”
Variations of the Barometer.—The variations observed in the pressure of the air may be divided into two classes, viz., periodical and irregular; the periodical variations recurring at regular intervals, whilst the irregular variations observe no stated times. The most marked of the periodical variation is the daily variation, the regularity of which in the tropics is so great that, according to Humboldt, the hour may be ascertained from the height of the barometer without an error of more than 15 or 17 minutes on the average. This [Pg 9] horary oscillation of the barometer is masked in Great Britain by the frequent fluctuations to which the atmosphere is subjected in these regions. It is, however, detected by taking the mean of a series of hourly observations conducted for some time. The results show two maxima occurring from 9 to 11 a.m. and from 9 to 11 p.m., and two minima occurring from 3 to 5 a.m. and from 3 to 5 p.m. (See Table, page 10.)
The maxima occur when the temperature is about the mean of the day, and the minima when it is at the highest and lowest respectively.
This daily fluctuation of the barometer is caused by the changes which take place from hour to hour of the day in the temperature, and by the varying quantity of vapor in the atmosphere. [Pg 10]
Table Showing the Daily Variations and Range of the Barometer in Different Latitudes.
| Lat. | A.M. | P.M. | Range. | |||
|---|---|---|---|---|---|---|
| Min. | Max. | Min. | Max. | |||
| Inches. | Inches. | Inches. | Inches. | Inches. | ||
| Atlantic Ocean | 0.0 | -.056 | +.069 | -.045 | +.045 | .125 |
| Pacific Ocean | 0.0 | -.032 | +.040 | -.045 | +.028 | .085 |
| Sierra Leone | 8.28 N. | -.022 | +.032 | -.038 | +.031 | .070 |
| Lima | 12.3 S. | -.071 | +.065 | -.067 | +.050 | 136 |
| Calcutta | 22.36 N. | -.017 | +.052 | -.038 | +.018 | .090 |
| Pekin | 39.53 N. | -.038 | +.047 | -.052 | +.014 | .099 |
| Great St. Bernard | 45.51 N. | -.010 | +.005 | -.003 | +.012 | .022 |
| Plymouth (England) | 50.21 N. | -.007 | +.006 | -.010 | +.010 | .020 |
| St. Petersburg | 59.58 N. | -.003 | +.008 | -.004 | +.002 | .012 |
[Pg 11] The surface of the globe is always divided into a day and night hemisphere, separated by a great circle which revolves with the sun from east to west in twenty-four hours. These two hemispheres are thus in direct contrast to each other in respect of heat and evaporation. The hemisphere exposed to the sun is warm, and that turned in the other direction is cold. Owing to the short time in which each revolution takes place, the time of greatest heat is not at noon, when the sun is in the meridian, but about two or three hours thereafter; similarly, the period of greatest cold occurs about four in the morning. As the hemisphere under the sun’s rays becomes heated, the air, expanding upwards and outwards, flows over upon the other hemisphere where the air is colder and denser. There thus revolves round the globe from day to day, a wave of heat, from the crest of which air constantly tends to flow towards the meridian of greatest cold on the opposite side of the globe.
The barometer is influenced to a large extent by the elastic force of the vapor of water invisibly suspended in the atmosphere, in the same way as it is influenced by the dry air (oxygen and hydrogen). But the [Pg 12] vapor of water also exerts a pressure on the barometer in another way. Vapor tends to diffuse itself equally through the air; but as the particles of air offer an obstruction to the watery particles, about 9 or 10 a.m., when evaporation is most rapid, the vapor is accumulated or pent up in the lower stratum of the atmosphere, and being impeded in its ascent its elastic force is increased by the reaction, and the barometer consequently rises. When the air falls below the temperature of the dew-point, part of its moisture is deposited in dew, and since some time must elapse before the vapor of the upper strata can diffuse itself downwards to supply the deficiency, the barometer falls—most markedly at 10 p.m., when the deposition of dew is greatest.
Hence, as regards temperature, the barometer is subject to a maximum and minimum pressure each day—the maximum occurring at the period of greatest cold, and the minimum at the period of greatest heat. And as regards vapor in the atmosphere, the barometer is subject to two maxima [Pg 13] and minima of pressure—the maxima occurring at 10 a.m., when, owing to the rapid evaporation, the accumulation of vapor near the surface is greatest, and about sunset, or just before dew begins to be deposited, when the relative amount of vapor is great; and the minima in the evening, when the deposition of dew is greatest, and before sunrise, when evaporation and the quantity of vapor in the air is least.
Thus the maximum in the forenoon is brought about by the rapid evaporation arising from the dryness of the air and the increasing temperature. But as the vapor becomes more equally diffused, and the air more saturated, evaporation proceeds more languidly; the air becomes also more expanded by the heat, and flows away to meet the diurnal wave of cold advancing from the eastwards. Thus the pressure falls to the afternoon minimum about 4 p.m. From this time the temperature declines, the air approaches more nearly the point of saturation, and the pressure being further increased by accessions of [Pg 14] air from the warm wave, now considerably to the westward, the evening maximum is attained. As the deposition of dew proceeds, the air becomes drier, the elastic pressure of the vapor is greatly diminished, and the pressure falls to a second minimum about 4 a.m.
The amount of these daily variations diminishes from the equator towards either pole, for the obvious reason that they depend, directly, or indirectly, on the heating power of the sun’s rays. Thus, while at the equator the daily fluctuation is 0.125 inch, in Great Britain it is only a sixth part of that amount. It is very small in the high latitudes of St. Petersburg and Bossekop; and in still higher latitudes, at that period of the year when there is no alternation of day and night, the diurnal variation probably does not occur. In the dry climate of Barnaul, in Siberia, there is no evening maximum; the lowest minimum occurs as early as midnight, and the only maximum at 9 a.m. [Pg 15]
Since the whole column of the atmosphere, from the sea level upwards, expands during the heat of the day, thus lifting a portion of it above all places at higher levels, it is evident that the afternoon minimum at high stations will be less than at lower stations, especially when the ascent from the one to the other is abrupt. Thus, at Padua, in Italy, the afternoon minimum is 0.014 inch, but at Great St. Bernard it is only 0.003 inch.
Annual Variation.—When it is summer in the one hemisphere, it is winter in the other. In the hemisphere where summer prevails, the whole air being warmer than in the other hemisphere, expands both vertically and laterally. As a consequence of the lateral expansion there follows a transference of part of the air from the warm to the cold hemisphere along the earth’s surface; and, as a consequence of the vertical expansion, an overflow in the upper regions of the atmosphere in the same direction. Hence, in so far as the dry air of [Pg 16] the atmosphere is concerned, the atmospheric pressure will be least in the summer and greatest in the winter of each hemisphere. But the production of aqueous vapor by evaporation being most active in summer, the pressure on the barometer will be much increased from this cause. As the aqueous vapor is transferred to the colder hemisphere it will be there condensed into rain, and being thereby withdrawn from the atmosphere, the barometer pressure will be diminished; but the dry air which the vapor brought with it from the warm hemisphere will remain, thus tending to increase the pressure.
In the neighborhood of the equator there is little variation in the mean pressure from month to month. Thus, at Cayenne, the pressure in January is 29.903 inches, and in July 29.957 inches.
At Calcutta, 22° 36' N. lat., the pressure is 29.408 in July, and 30.102 in January, thus showing a difference of 0.694; and at Rio de Janeiro, 22° 57' S. lat., it is 29.744 in January (summer), and 29.978 [Pg 17] in July (winter), the difference being 0.234. The large annual variation at Calcutta is caused jointly by the great heat in July, and by the heavy rains which accompany the south-west monsoons at this season; while in January the barometer is high, owing to the north-east monsoons, by which the dry cold dense air of Central Asia is conveyed southward over India.
At places where the amount of vapor in the air varies little from month to month, but the variations of temperature are great, the difference between the summer and winter pressures are very striking. Thus, at Barnaul and Irkutsk, both in Siberia, the pressures in July are respectively 29.243 and 28.267, and in January 29.897 and 28.865, the differences being upwards of six-tenths of an inch. The great heat of Siberia during summer causes the air to expand and flow away in all directions, and the diminished pressure is not compensated for by any material accessions being made to the aqueous vapor of the atmosphere; [Pg 18] and, on the other hand, the great cold and little rain in that region during winter causes high pressures to prevail during that season. The same peculiarity is seen, though in a modified degree, at Moscow, St. Petersburg, and Vienna.
At Reykjavik, in Iceland, the pressure in June is 29.717, and in December 29.273; at Sandwich, Orkney, 29.775, and 29.586; and at Sitcha, in Russian America, 29.975, and 29.664. In all these places the distribution of the pressure is just the reverse of what obtains in Siberia, being least in winter and greatest in summer. The high summer pressures are due to the cool summer temperatures as compared with surrounding countries, thus causing an inflow from these regions, and to the large amount of vapor in the atmosphere, thus still further raising the barometric column. On the other hand, the low winter pressures are due to the comparatively high winter temperatures causing an outflow towards adjoining countries, and the large [Pg 19] winter rainfall which, by setting free great quantitles of latent heat, still farther augments and accelerates the outflow.
The variations in mean pressure are very slight, and not marked by any very decided regularity in their march through the seasons, at Dublin, Glasgow, London, Paris, and Rome. As compared with Barnaul and Reykjavik their temperature is at no season very different from that of surrounding countries, and the vapor and rainfall are at no time much in excess or defect, but are more equally distributed over the different months of the year.
At the Great St. Bernard, 8174 feet above the sea, the pressure in summer is 22.364 inches, while in winter it is only 22.044. At Padua, there is scarcely any difference in the pressure between summer and winter. The increase in the summer pressure at the Great St. Bernard is no doubt due to the same cause already referred to in art. 65—viz., the expansion of the air upward during the warm summer months, thus [Pg 20] raising a larger portion of it above the barometer at the highest station. But at St. Fe de Bogota, 8615 feet high, near the equator, and where, consequently, the difference between the temperature in July and January is very small, the difference in the pressures of the same months is also very small, being only 0.035.
Distribution of Atmospheric Pressure over the globe, as determined by the Annual Means.—Though much additional observation is required, especially in Africa, Asia, and South America, before the isobarometric lines can be laid down on a map of the world, yet many important conclusions regarding the mean barometric pressure have been arrived at from the results already obtained. We have seen that the daily and monthly variations of pressure observed at different places are modified by the variations of the temperature of the air, the amount of vapor, and the rainfall. Since these are in their turn greatly modified by the unequal distribution of land and water on the earth’s surface, we should expect to find the pressure, and the [Pg 21] variations in the pressure, most regular in the southern hemisphere. Accordingly, there is a remarkable regularity observed in the distribution of the pressure from about 40° N. lat. southwards to the Antarctic Ocean, with the exception of the region of the monsoons in Southern Asia.
The mean pressure in the equatorial regions is about 29.90; at 20° N. lat. it rises to 30.00, and at 35° N. lat. to 30.20, from which northwards the pressure is diminished. The same peculiarity is seen south of the equator, but it is not so strongly marked. At 45° S. lat. it falls to 29.90, and from this southwards it continues steadily and rapidly to fall to a mean pressure of 28.91 at 75° S. lat. This extraordinary depression of the barometer in the Antarctic Ocean, being one inch less than at the equator and 1,326 inches less than at Algiers, is perhaps the most remarkable fact in the meteorology of the globe.
The pressure in the north temperate and frigid zones is in striking [Pg 22] contrast to the above. From Athens, in a north-eastern direction, a high isobarometric line traverses Asia, passing in its course Tiflis, Barnaul, Irkutsk, and Yakutsk. To the east of the northern part of this area of high mean pressure, around the peninsula of Kamtschatka, there is a region of low barometer, the mean pressure being only 29.682. There is another remarkable area of low pressure around Iceland, the center being probably in the south-west of the island near Reykjavik, where the mean is 29.578. As observations are more numerous in Europe and North America, the dimensions of this depression may be defined with considerable precision by drawing the isobarometric of 29.90, which is about the mean atmospheric pressure. This line passes through Barrow Straits in North America, thence south-eastward toward Newfoundland, then eastward through the north of Ireland, the south of Scotland, and the south of Sweden, whence it proceeds in a north-easterly direction to Spitzbergen. The following mean annual [Pg 23] pressures will show the nature of the depression: New York, 30.001; Paris, 29.988; London, 29.956; Glasgow, 29.863; Orkney, 29.781; Bergen, 29.804; Spitzbergen, 29.794; Reykjavik, 29.578; Godthaab, in S. Greenland, 29.605; Upernavik, in N. Greenland, 29.732; and Melville Island, 29.807. A depression also occurs in India, where the mean is only about 29.850, whereas in the same latitudes elsewhere it is about 30.100.
There are thus four areas of low pressure on the globe, the extent of each being nearly proportioned to the depth of the central depression—viz., Antarctic Ocean, the least pressure being 28.910; Iceland, 29.578; Kamtschatka, 29.682; and India, 29.850; and three areas of high pressure, one lying between latitudes 20° and 40° N., another between 15° and 35° S., and the third in Central Asia, from south-west to north-east. These low mean pressures are by no means constant in all cases during the months of the year. In the Antarctic Ocean they are nearly constant during the months, with perhaps a slight [Pg 24] tendency to an increase in winter. In the region of low pressure around Iceland the pressure is a little less than elsewhere in summer; but in winter, when the rainfall is heaviest, it is very much less, being 0.251 inch less in winter than in summer at Reykjavik, and 0.189 at Sandwich, in Orkney. Similarly at Petropaulovski, in Kamtschatka, the pressure in winter is 0.323 less than in summer. Hence the low mean annual pressures in the North Atlantic and the North Pacific are chiefly brought about by the low pressure during the cold months of the year, and are doubtless caused by the copious rainfall during that season. On the other hand, in Southern Asia, the lowest pressures occur in summer. Thus, at Calcutta it is 29.408 in July, while in January it is 30.102—the average pressure for that degree of north latitude. Hence, in Hindostan, the low mean annual pressure arises from the very low pressure in summer caused by the heavy rains falling at that season, particularly on the south slope of the Himalayas. Generally the [Pg 25] pressure is low wherever a copious rainfall prevails over a considerable portion of the earth’s surface, owing to the large quantity of caloric set free as the vapor is condensed into rain.
It is scarcely necessary to point out how important it is to keep in mind these facts of the pressure of the atmosphere, it being evident, for instance, that a pressure of 29.00 in the North Atlantic would portend stormy winds, while the same pressure south of Cape Horn, being the mean pressure there, would indicate settled weather.
The readings of the mercurial barometer are subjected in nice observations to several corrections:
1st. To 32° F. allowance being made for expansion of both mercury and scale for all observations above that temperature. A barometric pressure of thirty inches at 32° would be indicated by a height of 30⅒ inches at 70°.
[Pg 26]
2d. For decrease of gravitation at stations above the level of the sea, acting on both the mercury and the air.
3d. For increase of gravity with increase of latitude.
4th. For temperature of air; the density decreasing as temperature rises.
5th. For humidity of the air which also influences its density.
6th. For capillary attraction of the tube.
[Pg 27]
The text books in physics present formulas for computing heights from barometric observations, based on physical laws which we will briefly give.
If the density of the air were constant throughout, the measurement of heights would be a problem of the simplest character; for as mercury weighs 10,500 times as much as air at the sea level, the mercurial column would fall one inch for every 10,500 inches of ascent above the sea. But air is compressible, and, in accordance with Boyle’s law, its density varies with the pressure to which it is subjected.
Now suppose the atmosphere divided into layers of uniform thickness, but so thin that the density may be considered uniform throughout. [Pg 28]
Let h = the thickness of each layer.
W = weight of a cubic foot of air at pressure H.
W₁ = weight of a cubic foot of air at H.
H₀ H₁, &c. = pressures measured in inches of mercury.
Then the pressure upon the unit of surface of any layer is greater than that upon the surface of next higher layer, by the weight of a volume of air whose base is the unit of surface and whose height is the thickness of the layer. If one foot be the unit of surface, then this quantity would be hW. And to express it by height of mercury column, it is necessary to multiply by
which gives
But W : W₀ : : H : 30.
W₀ being the weight of a cubic foot air at the level of the sea (=.0807 at 32°F).
We have from the above
,
and the above expression for diminution may be written
.
[Pg 29] If H₀ H₁ H₂ represent the pressures at the surfaces of the successive layers, we shall have
Multiplying these equations and suppressing common factors, we get
If h be taken at one foot then n would represent the number of feet vertically between two stations at which the barometric pressures are Hn and H₀ respectively.
By substituting for W₀ its value and taking logarithms we have
whence
[Pg 30] For use in accurate observations, corrections are required for temperature, humidity and variation in the force of gravity.
La Place’s formula which includes terms derived from the consideration of these conditions is obtained as follows:
Suppose a portion of the atmosphere included between two stations at different altitudes to be divided into very thin laminæ.
Let z be the distance of one of these from the surface of the globe and dz its thickness.
Let P be the pressure upon a unit of surface upon the lower side of this layer; and W the weight per cubic meter of the air at this pressure.
Then the pressure on the upper side will be less than P by an amount equal to the weight of a column of air whose base is a unit and height is equal to dz.
Whence
If W₀ be the weight of a cubic meter of air at the temperature 0°C [Pg 31] and a barometric pressure of 0.ᵐ76, the weight of this same volume at pressure P and temperature ϴ would be
a being the coefficient of dilatation of air which is here taken at .004 in consequence of the constant presence of watery vapor.
This expresses the weight at the surface of the globe. If transferred to the height z, the weight would be diminished in the ratio of the squares of the distances from the center of the earth. We should then have
Substituting in equation 1, dividing by P and integrating between 0 and z, we get, by calling the pressure at the lower station P₀
the logarithm being Napierian.
From this we obtain [Pg 32]
But the pressures P₀ and P are in direct ratio of the mercury columns which we will designate by h₀ and h. These columns also vary in weight in accordance with the law of inverse squares of distance from the earth’s center, so that
Substituting in the value of z, we have
But as z is so very small compared with
R₁ we may replace by
.
Also may be neglected.
We shall then have
The weight W₀ refers to the height h₁ the lower of the two
[Pg 33]
stations. At the surface of the earth, this weight would be greater in
the ratio of . But as h is always small
compared with R this correction may be neglected.
But there is another of more importance which should be taken into account. On account of the spheroidal form of the globe weight varies with the latitude. If G represent the weight of a body at latitude 45°, then at any other latitude l, its weight, is found by multiplying G by
This factor is to be applied to W₀ in the formula. This is accomplished
by multiplying the above value of z by
In order to simplify the expression we will substitute for
the mean between the temperatures of the upper and lower stations,
designated by t₀ and t. The factor
then
becomes
and the value of z may be written [Pg 34]
If M be used to represent the modulus of the Napierian logarithms we may write
in which the logarithms are of the common kind.
This is La Place’s formula. h in the expression is not the barometric height directly observed at the upper station, but this height reduced to the temperature of the lower station.
The value of has been determined by trial of the
formula upon known altitudes. Ramond in his survey of the Pyrenees
determined its value to be 18336.
[Pg 35]
The unknown term z in the second member is determined by successive approximations.
The first value being
This being substituted, we may have
Finally, these being substituted in the above value of z we get
The terms of this formula are generally reduced to tabular form for practical use.
Guyot’s formula which is derived from this, reducing meters to feet and the constants depending on temperature being changed to accord with Fahrenheit’s scale, is
[Pg 36]
The three terms after the first are the corrections. The first being that for the temperature at the two stations. The second is the correction for the force of gravity depending on the latitude.
The third contains, first the correction for action of gravity on the mercury column at the elevation z, and second a correction required for decrease in density of air owing to decrease in action of gravity at the greater elevation. The factor s being the approximate difference in altitude of the stations.
Plantamour’s formula, which has been much used, differs slightly from Guyot’s. The first coefficient is 60384.3. The denominator of temperature term is 982.26 and a separate correction is used for humidity of the air.
To use either of these formulas tables are necessary, of which those [Pg 37] prepared by Lieut. Col. Williamson[1] are the most elaborate.
For the Aneroid in ordinary practice, formulas of much less complexity may be profitably used. The corrections depending upon the gravity of the mercury column would, in any case, be omitted. The other corrections may in very nice work be retained. But a correction depending on the effect of changes of temperature on the metallic work of the instrument should be carefully remembered. First-class Aneroids claim to be compensated, but a greater portion will need a correction which the purchaser can determine for himself, by subjecting the instrument to different temperatures while the pressure remains constant.
A modification of Guyot’s formula adapted to aneroid work was suggested in an excellent paper on the use of the aneroid, read before the American Society of Civil Engineers, in January, 1871. [Pg 38]
It is
D is the difference of altitude in feet. H and h are the barometric readings in inches.
T and t are the temperatures of the air at the two stations.
Table II is prepared for the use of this formula.
Other formulas will be given in another chapter.
[1] The use of the Barometer on Surveys and Reconnoisances. By R. S. Williamson. New York: D. Van Nostrand. London: Trubner & Co.
[Pg 39]
The general principle of construction of all aneroids is the same. A box with flexible sides, hermetically sealed, the air having been first exhausted, changes its form as the pressure of the atmosphere varies.
The chief differences in the various kinds lie in the mechanical devices, by which the motions of the box are rendered apparent to the eye, and also measured in such a manner as to allow the corresponding pressures to be expressed in inches of mercury. [Pg 40]
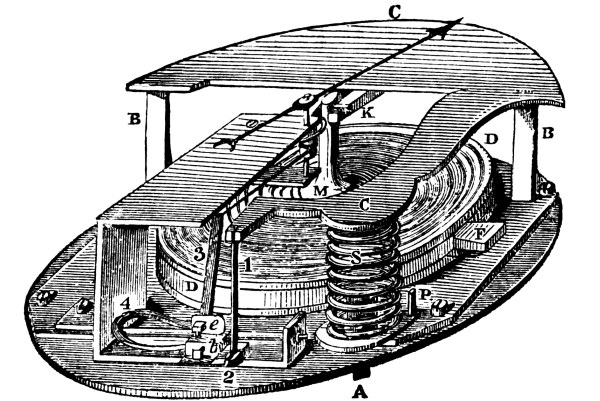
Fig. 1.
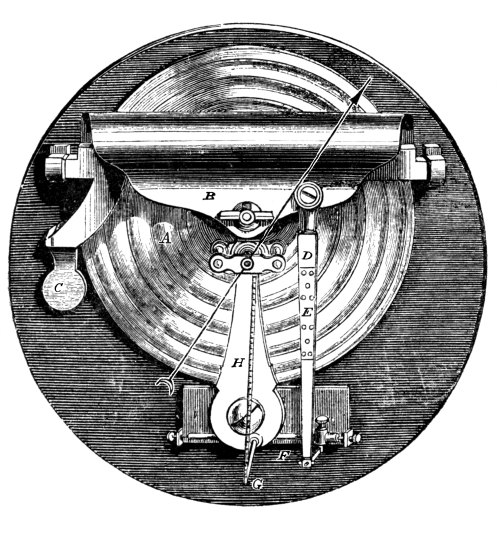
The aneroid was invented about the beginning of this century, but was first made of a serviceable form by Vidi, in 1848. It is substantially the form most used to-day. The vacuum box is a thin low cylinder, and the motion of the thin flexible head of the cylinder is conveyed by suitable mechanism to the index hand. Vidi’s aneroid is shown in Fig. 1. D is the vacuum box, supporting the upright pillar M upon its center. As M rises or falls, a corresponding motion is given to the [Pg 41] plate C. A counter-pressure is afforded by the spiral spring S. The motion of C is conveyed by the links 1 and 2 to a little rocker shaft, shown in the figure. An arm, 3, attached to this shaft is connected by a minute chain with the shaft which carries the index pointer. It is kept wound to the proper tension about this shaft by a fine spiral hair spring.
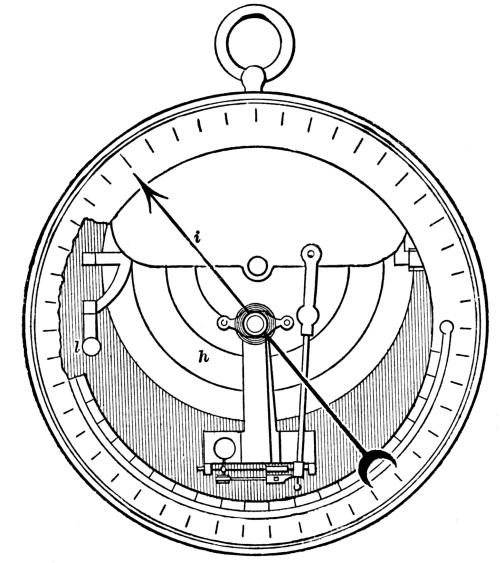
Fig. 2.
[Pg 42]
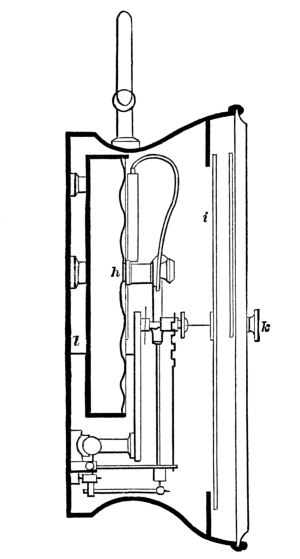
Fig. 3.
A modification of this is shown in Figs. 2 and 3. (See, also, frontispiece). This is Naudet’s aneroid, and is the one chiefly employed now. It differs from Vidi’s in the substitution of the thin [Pg 43] laminated spring (B in frontispiece) for the spiral spring (S in Fig. 1).
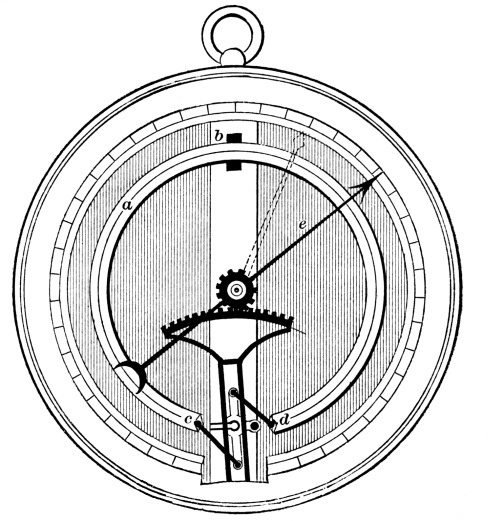
Fig. 4.
One of the oldest forms of box barometer and the one to which the name aneroid is restricted by some writers, is represented in Fig. 4. A rectangular tube, from which the air has been perfectly [Pg 44] exhausted, is sealed hermetically, and, having been bent into the form represented in the figure by cbd, is made fast at the middle point b. The varying pressure of the atmosphere causes the extremities c and d to approach or recede from each other. This motion is converted into a to-and-fro traverse of the index, by a mechanism sufficiently well exhibited by the diagram.
This is known as Bourdon’s form. It is not now employed for delicate work. The forms of Vidi and Naudet are, by some writers, designated the holosteric barometers.
The graduation of these instruments is made to correspond with the height of the mercurial barometer, and is expressed as inches or millimeters.
The difficulties to be met by the maker, in securing accuracy of working, are those which arise chiefly from the varying elasticity of the several metallic elements under change of temperature. Greater simplicity of construction might be presumed to be attended with a [Pg 45] smaller liability to a kind of error, for which it is exceedingly difficult to compensate. This is the theory of the Goldschmid Aneroid.
The instrument designed for ordinary engineering use is represented by Fig. 5. The size recommended by the present makers for this service is 3⅛ inches in diameter and 2½ inches high. [Pg 46]
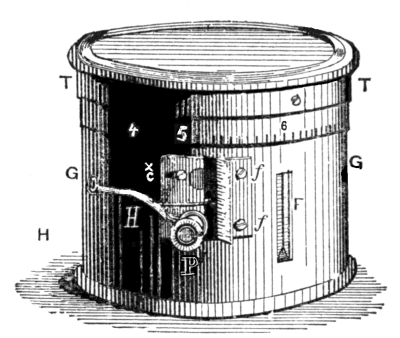
Fig. 5.
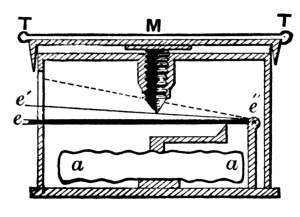
Fig. 6.
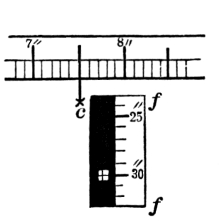
Fig. 7.
The construction is exhibited by Fig. 6. The vacuum box, constructed as before described, is shown at aa. The motions of the box, caused by variations of atmospheric pressure, are conveyed directly to the lever, whose fulcrum is at e″, and whose free end is at e. This end, projecting through the side of the casing and working freely through a slot, is observed with a magnifying lens, and the reading on the index ff taken. But it is evident that the lever, working with proper ease on its fulcrum, must be supplied with a certain amount of counter-pressure. This is ingeniously done by aid of the delicate spring e', which is attached to the lever near the fulcrum. Bearing on the spring is the point of the micrometer screw M, whose head is graduated to hundredths and forms the top of the case. Both lever and spring are furnished at their extremities with bright [Pg 47] metal heads, whose end surfaces lie in the same plane. The head e' is, under ordinary conditions, higher than e, as shown in Fig. 6. When a reading is to be taken the top of the case is turned until e' and e are side by side; the horizontal marks borne on the metallic heads being brought to an exact coincidence by aid of a lens (P in Fig. 5). The reading of the inches is taken from the scale ff, and of the hundredths from the divisions on the scale around the top of the box T; a fixed point c being marked on the cylinder. In figure 7 the indices exhibit a reading of 29.75 inches.
The thermometer F is an important part of the instrument.
In some of these instruments the scale ff bears no reference to the inches of the mercurial barometer, but is of an arbitrary character, and is different for different instruments. The value of the divisions is determined by comparison with standard instruments, and is carefully expressed in tabular form on the cover of the box. [Pg 48]
Some corrections for temperature and pressure are required in the use of these instruments which, although desirable in the more common forms of aneroid, have not heretofore been considered necessary. In the latter instruments, however, when of the best construction, a compensation has been effected which renders a correction for temperature unnecessary. In the Goldschmid aneroids no compensation is attempted, but each instrument is furnished with a table of corrections which have been prepared from observation on standard instruments.
Thus, aneroid No. 3187, imported last year, bears on the cover the following: [Pg 49]
CORRECTION TABLE.
| For Division. | For Temperature. |
| 26.0″ = -0.02 | 28° to 48° = 0 |
| 26.5″ = -0.03 | 52° = +0.01 |
| 27.0″ = -0.03 | 56° = +0.015 |
| 27.5″ = -0.02 | 60° = +0.025 |
| 28.0″ = 0 | 64° = +0.035 |
| 28.5″ = +0.03 | 68° = +0.04 |
| 29.0″ = +0.06 | 72° = +0.05 |
| 29.5″ = +0.10 | 76° = +0.07 |
| 30.0″ = +0.14 | 80° = +0.09 |
| 30.5″ = +0.19 | 84° = +0.11 |
| 31.0″ = +0.25 | 92° = +0.15 |
The temperatures are, of course, taken from the thermometer that forms a part of the instrument, and which, when the latter is carried slung from the shoulder, may exhibit a temperature considerably higher than that of the air.
A smaller and ruder instrument called the Pocket Aneroid is made by the Zurich manufacturers. It is only 1½ inches in diameter and 1¼ inches high. A bar fastened to the top of the vacuum box takes the place of the lever in the larger instrument.
A larger size is also made in which the movements of the vacuum box are directly observed with a compound microscope. [Pg 50]
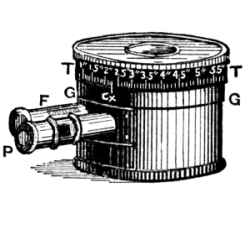
Fig. 8.
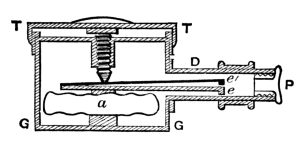
Fig. 9.
There is no doubt that all aneroids need a careful comparison with standard instruments or a series of trials upon known altitudes, in order to determine the proper corrections. Such trials should be made at different temperatures and under different conditions as to rising or falling at the time of observation. The tables of corrections [Pg 51] furnished by the maker cannot well be substituted for those made by a careful observer deduced from systematic work. The air pump, the hot chamber and the freezing box are convenient, but inadequate substitutes for a large number of trials under normal conditions.
[Pg 52]
The Aneroid, like the Mercurial barometer may be used either as a weather indicator or in the measurement of altitudes. When used in the former capacity, the Aneroid, especially at sea, possesses some obvious advantages. Aside from its superior compactness of form and its portability, it responds more readily to the changes in atmospheric pressure than the Mercury column, and thereby serves more efficiently to warn the mariner of sudden tempests.
The words Rain—Change—Fair seen stamped or engraved on the dial of many barometers have, of course, no special significance, and are now rarely seen on first-class instruments of either kind. The probable changes of weather indicated by changes of the barometer are briefly set forth in the following: [Pg 53]
RULES FOR FORETELLING THE WEATHER.
A Rising Barometer.
A “rapid” rise indicates unsettled weather.
A “gradual” rise indicates settled weather.
A “rise” with dry air, and cold increasing in summer, indicates wind from Northward; and if rain has fallen better weather is to be expected.
A “rise” with moist air, and a low temperature, indicates wind and rain from Northward.
A “rise” with southerly wind indicates fine weather.
A Steady Barometer.
With dry air and seasonable temperature, indicates a continuance of very fine weather.
A Falling Barometer.
A “rapid” fall indicates stormy weather.
A “rapid” fall, with westerly wind, indicates stormy weather from Northward. [Pg 54]
A “fall,” with a northerly wind, indicates storm, with rain and hail in summer, and snow in winter.
A “fall,” with increased moisture in the air, and the heat increasing, indicates wind and rain from Southward.
A “fall” with dry air and cold increasing (in winter) indicates snow.
A “fall” after very calm and warm weather indicates rain with squally weather.
It does not require the highest quality in the mechanism of an Aneroid to serve the purpose indicated in the above rules.
For the accurate measurement of differences of altitude, however, the best skill in construction and the most careful adjustment of the parts is indispensably necessary. The use of an Aneroid of even medium quality will frequently lead to considerable errors in estimating heights. It may also be added here that instruments of the best manufacture in the hands of observers unacquainted with the principles [Pg 55] involved, will often lead to erroneous conclusions. This is owing in many cases to a method adopted by some makers of adding a circle marked feet outside of the common graduation to inches of mercury.
Many tourists carry Aneroids of the pocket size, and consult them frequently while traveling, relying upon a single observation of the index for the determination of their altitude.
If such a circle of feet be engraved on the dial plate with the zero mark made to correspond with 30 inches of the mercury column, of course every estimate of altitude made as above mentioned assumes that at the moment of observation; the barometer at the level of the sea would stand exactly at 30 inches; a condition only realized occasionally. And the further condition is also assumed, that the temperature of the air is of no account in estimating heights; an assumption equally at variance with fact.
It is only an inferior class of Aneroids that bear a fixed graduated circle of feet, with the zero of altitude corresponding to 30 inches of pressure. [Pg 56]
Prof. Airy, the former Astronomer Royal of Great Britain, prepared a table for the use of barometer makers—a scale from which is now engraved on many English Aneroids. It places the zero of altitude at 31 inches of pressure. This affords such large numbers for slight elevations that the proper use of the rule is suggested to the observer. He is led to subtract the two readings of feet to get difference in height. But this again assumes that the average temperature is 50° F.
Table I exhibits Prof. Airy’s series of heights.
Some makers, designing to improve upon the simple construction just described, have engraved the outer circle of feet on a movable ring encircling the dial, so that when an observer is at any locality whose height is known, he may bring the proper mark of the altitude scale against the index pointer. Then if the observer travels about over a section of country, the pointer will indicate with fair approximation for some hours the altitude of the new positions.
[Pg 57] This device is convenient to a skilled observer who only requires rapid and approximate results, but to the novice it is misleading in two ways; first, because the temperature is left out of the calculation, and furthermore, such a use of the movable scale will, at times, involve a large error, as it is not a scale of equal parts.
Mr. Rogers Field, C. E., in 1873, applied the movable scale to the Aneroid, so as to convert it from a source of inaccuracy into an aid towards accuracy. He employs the altitude scale proposed by Sir G. Airy for temperature 50°, but he makes it movable so as to adjust it for any other temperature. The shifting of the scale into certain fixed positions, is made to answer the same purpose as if the original scale were altered to suit various temperatures of the air. In the Journal of the Meteorological Society for 1874, January, Mr. Field says:
“The object aimed at in designing this improved form of Aneroid was, to [Pg 58] simplify the correct determination of altitudes in cases such as ordinarily occur in England, and the instrument is therefore arranged to suit moderate elevations, say of 2000 feet and under, and is not intended for more considerable heights.
“The Aneroid is graduated for inches in the usual way on the face, but the graduation only extends from 31 inches to 27 inches so as to preserve an open scale. The outer movable scale is graduated in feet for altitudes, and this graduation is laid down by fixing the movable scale with the zero opposite 31 inches. This is the normal position of the scale and it is then correct for a temperature of 50°. For temperatures below 50° the zero of the scale is moved below 31 inches; for temperatures above 50°, the zero of the scale is moved above 31 inches. The exact position of the scale for different temperatures has been determined partly by calculation and partly by trial, and marked by figures engraved on the outside of the Aneroid. In order to insure the altitude scale not being shifted, after it has once been set in its [Pg 59] proper position there is a simple contrivance for locking it in the various positions. This consists of a pin, which fits into a series of notches on the outside of the ring carrying the glass. By slightly raising the glass it is freed from this locking pin, and can be turned until the figures corresponding to the air temperature are opposite to the pin, when the glass should be depressed so as to relock it, and the scale becomes correct for that temperature. The altitudes are in all cases determined by taking two readings, one at each station, and then subtracting the reading at the lower station from that at the upper.
“It will be seen from the foregoing description that the movable scale of the instrument requires to be set for temperatures before taking any observations, and must not be shifted during the progress of the observations.
“This may appear at first sight as a defect, inasmuch as the temperature of the air may alter during the progress of the observations; but practically it will not be found to be any drawback [Pg 60] in the case of moderate altitudes, as small variations of temperature will not appreciably affect the result. A variation of 5° of temperature gives only about 1 per cent. variation in the altitude, an amount that would under ordinary circumstances be inappreciable, so that as long as the temperature does not vary during the course of the observations more than 5° from that at which the instrument is set, the results may be accepted as correct, and, generally speaking, even a greater variation than this, say 6° or 8°, would be practically of no importance. Of course, if it should be found at any time that the temperature has varied considerably, during the course of the observations, from that at which the instrument was set, this variation can be allowed for by calculation in the usual way.”
The principle of allowing for variation of temperatures of the air by shifting the altitude scale is not theoretically accurate, but sufficiently so for practical purposes. For altitudes within the range [Pg 61] of the instrument (say 3000 feet and under) and temperatures between 30° and 70°, the maximum error from using the shifted scale, instead of the calculation, is only 2 feet, which is inappreciable on the scale. The same principle might even be applied to altitudes up to 6000 feet, as the maximum error would be only 10 feet. For considerable elevations, however, the variations of the temperature between the base and the summit would interfere with the application of the principle.
Nevertheless, the best plan is to dispense with altitude scales, whether fixed or movable, and to calculate the heights. Simple rules, giving more reliable results than the attached scales, are at the service of those who need easy processes. Among these are the following:
Note the rise or fall of the barometer in hundredths of an inch, in passing from one station to the other; multiply by 9. The product is the difference of altitude in feet.
This is for ordinary temperatures and pressures. If the pressure is [Pg 62] below 26 inches or the temperature above 70°, use 10 for a multiplier.
A higher degree of accuracy is obtained by using the multiplier obtained from the following table prepared by Mr. G. J. Symons:
| Mean temperature | 30° | 40° | 50° | 60° | 70° | 80° |
|---|---|---|---|---|---|---|
| Mean pressure, 27in. | 9.7 | 9.9 | 10.1 | 10.3 | 10.6 | 10.8 |
| ””28in. | 9.3 | 9.5 | 9.8 | 10.0 | 10.2 | 10.4 |
| ””29in. | 9.0 | 9.2 | 9.4 | 9.6 | 9.8 | 10.0 |
| ””30in. | 8.7 | 8.9 | 9.1 | 9.3 | 9.5 | 9.7 |
To find the difference in height between two stations: Find the mean pressure; also the mean temperature. The number in the table corresponding to these two means, if multiplied by the difference of the barometric pressures in hundredths of an inch, will give the difference in altitude very nearly.
In the absence of a table to aid in computation, but having an Aneroid with the scale of feet, use the formula,
[Pg 63]
adding of the estimated altitude for every degree,
the average temperature is above 55°, and subtracting a like
amount when it is below. D, is the difference of altitude in feet; H
and h are the readings in feet from the Aneroid scale.
This gives fair approximations up to 3000 feet.
For accurate results use one of the following methods: Having Airy’s table (Table 1) and an Aneroid carefully graduated to inches; Take the reading in inches of the barometric scale at both lower and upper stations; also the temperature at both stations. Find from the table the heights in feet corresponding to the barometer readings. Subtract them and multiply the remainder by
The complete formula is
T and t are the observed temperatures; H and h are the heights in feet taken from the table. [Pg 64]
In the absence of this table, but with a table of logarithms at hand, the barometric heights in inches are to be taken, and the following formula used:
B and b are the barometric readings in inches; D, T and t as in the other formulas. (See Table II.)
To avoid error from the constant changes in barometric pressure, the observations should be simultaneous. This is accomplished in the best manner by using two instruments, and requires, when the distance between the stations is considerable, two observers. With one instrument only, large errors are avoided by repeating the observation at the first station after taking that at the 2d station, and assuming that any change in barometric pressure that has occurred has been gradual during the absence.
When it is impracticable to repeat the observation at the first [Pg 65] station, the error which, in case of a changing pressure, might be a large one, may be reduced if the observation at the 2d station be continued for an hour or two, or until the rate of change can be estimated and a proportionate correction applied.
Many Aneroids marked “compensated” exhibit a sensible change when the temperature is varied; such instruments may be serviceable and quite accurate if allowance be made for the error of the instrument. This correction the owner had better determine by experiment. It is easy to subject the Aneroid to such variation of temperature as shall embrace the range at which it is likely to be used, and the movement of the index for each 10° or 20° of temperature recorded.
Aneroids require to be compared from time to time with a good mercurial barometer. While making such comparisons, it is well to remember that the mercurial column and the scale by which it is measured both require correcting, and that during times of rapid changes, in atmospheric [Pg 66] pressure, the Aneroid shows such changes more readily than the mercurial barometer. (See Table IV.)
In measuring heights with the Aneroid care should be taken that the instrument is not influenced by the heat of the hand nor by the direct rays from the sun.
The instrument should always be tapped gently with the finger at the moment of taking an observation. It should also be held in the same position for both observations; preferably with the face horizontal.
Considerable care is also required to determine exactly where the index points. It is best accomplished by sighting along the pointer, using one eye only for the purpose.
The following example will illustrate the use of the tables.
| Barometer at Station A | 30.04 | Thermometer 78° |
| ” ” ” B | 28.68 | ” 65° |
From Table I we find height corresponding to reading at A is 857 feet. The height for B is 2120 feet.
[Pg 67]
The approximate height is 2120-857 = 1263 feet; but the sum of the
temperatures is 143°. An additional correction of
is, therefore, to be applied to the above difference; this is 54 feet.
The total estimated difference of altitude is then 1263 + 54 = 1317 feet.
The formula directly applied is
Applying the logarithmic formula we have:
As before remarked, the Goldschmid Aneroid requires that both the temperature of the air and of the instrument be carefully taken. Two examples of altitudes taken with the instrument previously referred to (No. 3187) will serve to show the kind of correction necessary, and as [Pg 68] both examples apply to the same mountain (Kiarsarge of Conway, N. H.,) they will together indicate the character of the instrument
Ex. I.—July 9th, 1881.
| Station. | Time | Bar. Reading. |
Temp. | Correct’ns | Corrected Reading. |
||
|---|---|---|---|---|---|---|---|
| Air. | Inst. | Temp. | Press. | ||||
| Freyb’g. | 6.00 a.m. | 29.51 | 66° | 66° | +.04 | -.10 | 29.65 |
| Mt. Kiarsarge. | 1.00 p.m. | 26.75 | 74° | 74° | +.06 | -.03 | 26.78 |
Ex. II.—August 9th, 1881.
| Station. | Time | Bar. Reading. |
Temp. | Correct’ns | Corrected Reading. |
||
|---|---|---|---|---|---|---|---|
| Air. | Inst. | Temp. | Press. | ||||
| Freyb’g. | 7.00 a.m. | 29.34 | 60° | 65° | +.03 | +.09 | 29.46 |
| Mt. Kiarsarge. | 1.20 p.m. | 26.48 | 65° | 75° | +.06 | -.03 | 26.51 |
In both these examples another reading would have been taken at Fryeburg [Pg 69] on the return, if the better alternative of securing hourly readings of a stationary barometer at Fryeburg had not been followed. On July 9th there was no change in the Fryeburg barometer. On August 9th the following readings were taken at Fryeburg:
| 7 | A.M. | 29.53 |
| 8 | ” | 29.52 |
| 10 | ” | 29.515 |
| 12 | ” | 29.46 |
| 1 | P.M. | 29.46 |
| 2 | ” | 29.455 |
| 3 | ” | 29.40 |
As this set of observations indicates a fall of .07 in the interval between the base and summit readings, it becomes necessary to make another correction to the last column.
Correcting the first reading to accord with the fall indicated by the stationary barometer, we get after all corrections:
| Fryeburg, | 29.39 |
| Mt. Kiarsarge, | 26.51 |
The logarithmic formula for estimating heights from barometric observations is
in which [Pg 70]
| D | = | difference in altitude in feet. |
| B | = | height of barometer in inches at lower station. |
| b | = | height of barometer in inches at upper station. |
| T and t are the temperatures of the air in Fahrenheit degrees. | ||
Applying this formula to our first example we have:
The second example gives:
As the station at Fryeburg is 434 feet above the sea, the estimated total height of Kiarsarge would be, in one case, 3321 feet, and in the other 3315 feet.
Prof. Airy’s table gives 3319 and 3314 from the same data.
The instrument employed in the above measurements has been used in many [Pg 71] other cases of altitudes from 3000 to 4000 feet. An error of about 2 per cent. in excess has been detected in those cases where the altitude has been measured by more accurate means. It seems likely that the special correction needs some slight revision.
The following measurement was made with an aneroid only 1½ inches diameter, made by Casella.
Neversink, Sullivan Co., N. Y.,
and Slide Mountain, Ulster Co.
| Time. | Bar. Readings |
T. | Ht. Tab. I. |
|
|---|---|---|---|---|
| Neversink. | 7 a.m. | 28.64 | 61° | 2158 |
| Fly Club Camp. | 11 ” | 27.92 | 78° | 2853 |
| Slide Mountain. | 4 p.m. | 25.87 | 69° | 4931 |
As Neversink had been satisfactorily determined to be 1350 feet above the sea, the total height of Slide Mountain is estimated from this observation to have an altitude of 4206 feet. [Pg 72]
(Note).—Return observations were made only at the camp of the Fly Club. Between 11 a.m. and 9 p.m., no change occurred in the barometer.
The Tribune report, however, indicates a rise on this date of .07 between 7 and 11 a.m. If such a change was felt in this region, then the calculated height of the mountain is too low by at least 60 feet. On the other hand, a height given by railway survey in this vicinity, (Johnson’s Mill) near the camp, seems to confirm the figures given here.
Also, the height of Helsinger Notch, taken incidentally on this excursion, was estimated at 2660 feet. Guyot makes the Notch 2677 and the summit of Slide Mountain 4205 feet.
The height of the base at Neversink was established by four observations, between New York Bay and this base, and was confirmed by comparison with the height of the railway track at Liberty, six miles south-west. [Pg 73]
Neversink to Blue Mountain,
August 18, 1880.
| Time. | Bar. Readings |
T. | Cor. Rd’g. |
Ht. Tab. I. |
|
|---|---|---|---|---|---|
| Neversink. | 10:30 p.m. | 28.90 | 60° | 28.87 | 1941 |
| Blue Mt. | 3 p.m. | 27.47 | 60° | 27.47 | 3295 |
| Neversink | 6” | 28.85 | 64° | ||
The corrected reading would be 28.875, if the second reading had been midway in point of time between the first and last.
This mountain is in Ulster Co., N. Y. Long. 74° 35 W, and Lat. 41° 52 N.
Neversink and Denman Mountains (Casella Aneroid).
September 11, 1880.
| Time. | Bar. Readings |
T. | Cor. Rd’g. |
Ht. Tab. I. |
|
|---|---|---|---|---|---|
| Neversink. | 12:30 a.m. | 28.86 | 70° | 28.84 | 1969 |
| D. Mt. | 4:30 ” | 27.13 | 63° | 27.13 | 3634 |
| Neversink | 9 ” | 28.82 | 55° | ||
[Pg 74]
This mountain is S. S. W. of Slide Mountain, and near Claraville. Long. 74° 28'; Lat. 41° 53' N.
Fryeburg, Me., and Kiarsarge Mountain, N. H.—Fryeburg base 434 feet above the sea, July 9th, 1881.
(Casella Aneroid)
| Time. | Bar. Readings |
T. | Ht. Tab. I. |
|
|---|---|---|---|---|
| Fryeburg | 6 a.m. | 29.63 | 66° | 1233 |
| Kiarsarge | 1 p.m. | 26.83 | 74° | 3938 |
(Note)—Barometer at Fryeburg remained stationary.
[Pg 75] Fryeburg, Me., and Mt. Kiarsarge, N. H. (second survey) August 17th, 1881.
(Casella Aneroid.)
| Time. | Bar. Readings |
T. | Ht. Tab. I. |
|
|---|---|---|---|---|
| Fryeburg | 9 a.m. | 29.70 | 59° | 1169 |
| Mt. Kiarsarge | 3 p.m. | 26.81 | 53° | 3958 |
(Note)—Barometer at Fryeburg stationary till 4 p.m.
Diff. = 2,789 × 1.012 = 2822 feet.
Total ht. = 3256 feet above the sea.
Height of this summit according to the Geological Survey is 3251 feet.
Liberty Hill, N. H. (near Laconia), and Mt. Belknap.—The base station was at Mr. Rowe’s 1130 feet above the sea, July 9th, 1878.
(Casella Barometer.)
| Bar. Readings |
T. | Ht. Tab. I. |
|
|---|---|---|---|
| Liberty Hill | 28.75 | 82° | 2054 |
| Mt. Belknap | 27.53 | 79° | 3235 |
[Pg 76] As the interval between the observations was very short, and the general pressure sensibly stationary, no record was made of the time nor the return reading.
(Note)—An average of three measurements of this mountain gave 2392 feet. The other observations yielding 2369 and 2425 ft. respectively.
The height given in the Guide Books quoted from the Geological Survey is 2394 feet.
[Pg 77]
Dealers in good aneroids are generally prepared to testify in regard to the performance of their instruments when tested by the air pump. Comparison tables frequently accompany first-class instruments which show the differences between the aneroid referred to and a standard mercurial barometer submitted to the same exhaustion.
The buyer may reasonably ask, therefore, that such a test may be made if it has not been previously done.
The best English aneroids are now marked compensated, and are presumably free from error arising from changes of temperature in the instrument itself. Whether such be the case can readily be determined, [Pg 78] by the owner of the instrument subjecting it to the action of a freezing mixture and then of a drying oven, while the normal pressure remains the same. A thermometer should be placed beside the aneroid during the trial. A range of temperature from 15° F. to 175° F. may easily be produced, and a coefficient of correction if the instrument is not compensated, may be determined.
The graduations of a good instrument are neatly engraved on the dial.
The divisions corresponding to the inches and fractions of a mercurial barometer are the only essential ones. The circle of feet, whether movable or fixed, is a convenience of secondary importance.
If an aneroid bears a fixed circle of feet with the zero mark corresponding to the 30-inch point of the other scale, the probabilities are that the instrument is not from one of the best makers.
Excellent aneroids are now made with dial plates only 2½ inches in diameter. The Casella barometer referred to in the examples has a [Pg 79] diameter of only 1¼ inches. Of course the smaller fractions of an inch are more easily read on dials of 4 inches in diameter; but the portability of the smaller instruments recommends them for the use of the topographer, and the medium size, which is from 2¼ to 2½ inches, is now most in demand for surveyor’s work.
The aneroids in any considerable collection will be found to be variously graduated; some of them capable of indicating a fall of pressure to 20 inches, corresponding to a height of over 11,000 feet, while many are designed for continual use below 3,000 feet of altitude. In two instruments of the same diameter, but differing as above, it is clear that the latter will have the larger scale divisions, and will, therefore, be the better instrument to use at the lower altitudes.
It should be carefully remembered that all aneroids vary in their readings, with the position in which they are held; reading always a [Pg 80] little higher with the dial horizontal (face uppermost), than when it is vertical. The difference is clearly owing to the direct weight of the mechanism exerted on the vacuum box. There is no objection to allowing this weight to be always added, but the practice of the observer should be uniform, and to read from the horizontal dial is probably the most convenient practice.
A tap with the finger just before taking the reading is required to bring the springs to their proper bearing. Also, in case of rapid ascents, as some aneroids will not, at the moment of attaining an altitude, indicate the entire fall of pressure, a few minutes’ delay is necessary.
The pointer should be fine and very close to the graduated scale, and the reading should be taken by looking along the direction of the pointer.
For ordinary work it should not be considered important to adjust the aneroid to an absolute agreement with the mercurial barometer. The difference between the readings may be noted, but to force the aneroid [Pg 81] to an agreement by aid of the adjusting screw is a questionable practice.
Whenever comparison with the mercury column is made, the reduction for the latter by Table 4 should be carefully observed.
In the use of either form of Aneroid, whether it has been furnished with a correction or not, the observer should take early means to become acquainted with its limits of error under various conditions of temperature or pressure. Repeated measurements of a known altitude afford good data for such information, but direct comparisons, for a long time, with a standard cistern barometer will yield, with a minimum of labor, the greatest number of comparisons.
For the method of dealing with such data to determine correction coefficients, the reader is referred to the larger treatises, the most exhaustive of which, probably, is “Die Aneroide,” by Josef Höltschl (Alfred Holder, Vienna, 1872). [Pg 82]
For ordinary use of a single instrument, however, the corrections, if any are necessary, are determined with sufficient accuracy by the exercise of ordinary skill and patience; skill here implying, also, systematic trial.
Some of the sources of error in measuring altitudes, which are not to be eliminated by any adjustment or correction of instruments, are clearly stated by Prof. Elias Loomis, in a paper read before the National Academy of Sciences, April 19, 1881.
“The Laplace formula assumed that the atmosphere has attained a condition of equilibrium, and in such a case it gives the reduction to sea level with tolerable accuracy. The average of a long series of observations represents approximately such a condition of equilibrium; but in the daily observations this equilibrium is very much disturbed. The mean between the temperatures at the upper and lower stations does not represent the average temperature of the intermediate column of [Pg 83] air; and when the atmosphere is in rapid motion the downward pressure is modified by the earth’s rotation, in a manner not represented by the Laplace formula. There is no doubt that the formulæ of reduction now employed may be considerably improved; but it does not seem possible that any single formula, with constant coefficients, should provide for the immense variety of conditions which prevail in the neighborhood of mountain stations; and we may be compelled for each mountain region to adopt tables founded upon a direct comparison of observations made at stations of different elevations and not very remote from each other.”
The following remarks bearing upon the same subject are from an article by J. Allan Brown, F. R. S., on “Periodic Oscillations of Barometric Pressure,” published in Nature in April, 1881:
Sedgwick has said: [“To explain difficulties in these questions” (relating to pressure and temperature) “the atmospheric strata have been shuffled in accordance with laboratory experience.”] [Pg 84]
“If we suppose that the attraction of gravity is not the only attraction which affects the pressure of the atmosphere, but that this pressure varies through some other attracting force—such as an electric attraction of the sun depending upon the varying humidity of the air, and this again depending on its temperature, we should find another method of relating the two variations which does not exist if gravitation alone is employed. It is quite certain that many physicists will not admit the idea of an electric attraction on our atmosphere in the present state of our knowledge, hence the efforts to make expansion, and a shuffling of the atmospheric strata suffice. We must not, however, in our ignorance, attempt to force conclusions in opposition to facts, and if these can be satisfied more easily and with greater probabilities in its favor by the aid of the hypothesis of an electric attraction of the sun, that hypothesis will have a better claim to acceptance than the other. I shall here note a few facts which cannot be explained by thermic actions. [Pg 85]
“1. I have shown that, on the average of many years’ observation in our latitudes, the mean pressure diminishes at the rate of 0″.038 of mercury for every one hundred miles we proceed toward the north. This has been called a gradient from the similar term used in railway slopes: but it is no slope, it is a level of a surface of equilibrium like that of the sea. It is the mean heights of the barometer at the sea level which indicate the form, if we may so say, of the equilibrating atmosphere.
“2. In India we have seen that the atmospheric pressure oscillates at each station even when these are quite near to each other, independently of the known laws of equilibrium of gases. When we turn to the semi-diurnal oscillation of the barometer we are only amused at the attempts made to explain it by shuffling the atmospheric strata. Nothing can be more certain than that the theories of expansion, or resistance to expansion and overflow, are the vain efforts to make the [Pg 86] laws of nature agree with a theory. Over the great ocean within the tropics, where the diurnal variations of temperature are small and the air is absolutely without perceptible currents for days together, the barometer rises and falls a tenth of an inch twice in twenty-four hours with the regularity of the solar clock. The action of the sun on the whole atmosphere which produces this movement varies chiefly during the day hours at inland stations with the temperature oscillation, so that, as in the case of the annual variation, the fall of the barometer at 4 p.m. is greater in the same latitude as the temperature is higher. This variation occurs during the most complete calms; the smoke rises vertically from the plain of Tinnevelly; no current is visible in the motion of the clouds; yet the barometer falls at four in the morning as it did at four in the afternoon, only it falls less.”
It seems probable that the use of the Aneroid will soon become more widely extended, and that engineers, when made familiar with the [Pg 87] qualities of well-made instruments, will welcome so valuable an aid in preliminary surveys. The conditions of satisfactory work with barometers are certainly peculiar, and to field workers familiar only with the level and transit, may seem unique. But when the conditions are fully understood, the engineer may easily take precautions which will avoid too large errors, and conduct surveys in hilly regions with a celerity not heretofore attained.
[Pg 88]
Take readings of the barometer and thermometer
at both stations; find in the the heights corresponding to the
barometric readings, and subtract them. Multiply the remainder by
. T and t being the temperatures,
the product will be the difference in altitude.
| Barometer Readings. |
Heights. |
| Inches. | Feet. |
| 31.00 | 00 |
| 30.99 | 9 |
| 30.98 | 18 |
| 30.97 | 27 |
| 30.96 | 35 |
| 30.95 | 44 |
| 30.94 | 53 |
| 30.93 | 62 |
| 30.92 | 71 |
| 30.91 | 80 |
| 30.90 | 88 |
| 30.89 | 97 |
| 30.88 | 106 |
| 30.87 | 115 |
| 30.86 | 124 |
| 30.85 | 133 |
| 30.84 | 142 |
| 30.83 | 151 |
| 30.82 | 160 |
| 30.81 | 168 |
| 30.80 | 177 |
| 30.79 | 186 |
| 30.78 | 195 |
| 30.77 | 203 |
| 30.76 | 212 |
| 30.75 | 221 |
| 30.74 | 230 |
| 30.73 | 239 |
| 30.72 | 247 |
| 30.71 | 256 |
| 30.70 | 265 |
| 30.69 | 274 |
| 30.68 | 283 |
| 30.67 | 292 |
| 30.66 | 301 |
| 30.65 | 310 |
| 30.64 | 318 [Pg 89] |
| 30.63 | 327 |
| 30.62 | 336 |
| 30.61 | 345 |
| 30.60 | 354 |
| 30.59 | 363 |
| 30.58 | 372 |
| 30.57 | 381 |
| 30.56 | 390 |
| 30.55 | 399 |
| 30.54 | 407 |
| 30.53 | 416 |
| 30.52 | 425 |
| 30.51 | 434 |
| 30.50 | 443 |
| 30.49 | 452 |
| 30.48 | 461 |
| 30.47 | 470 |
| 30.46 | 479 |
| 30.45 | 488 |
| 30.44 | 497 |
| 30.43 | 506 |
| 30.42 | 515 |
| 30.41 | 524 |
| 30.40 | 533 |
| 30.39 | 542 |
| 30.38 | 551 |
| 30.37 | 559 |
| 30.36 | 569 |
| 30.35 | 578 |
| 30.34 | 587 |
| 30.33 | 596 |
| 30.32 | 605 |
| 30.31 | 613 |
| 30.30 | 622 |
| 30.29 | 631 |
| 30.28 | 640 |
| 30.27 | 649 |
| 30.26 | 658 |
| 30.25 | 667 |
| 30.24 | 676 |
| 30.23 | 685 |
| 30.22 | 694 |
| 30.21 | 703 |
| 30.20 | 712 |
| 30.19 | 721 |
| 30.18 | 730 |
| 30.17 | 740 |
| 30.16 | 749 |
| 30.15 | 758 |
| 30.14 | 767 |
| 30.13 | 776 |
| 30.12 | 785 |
| 30.11 | 794 |
| 30.10 | 803 |
| 30.09 | 812 |
| 30.08 | 821 |
| 30.07 | 830 |
| 30.06 | 839 |
| 30.05 | 849 |
| 30.04 | 857 |
| 30.03 | 866 |
| 30.02 | 875 |
| 30.01 | 884 |
| 30.00 | 893 [Pg 90] |
| 29.99 | 903 |
| 29.98 | 911 |
| 29.97 | 920 |
| 29.96 | 929 |
| 29.95 | 938 |
| 29.94 | 947 |
| 29.93 | 956 |
| 29.92 | 965 |
| 29.91 | 976 |
| 29.90 | 985 |
| 29.89 | 994 |
| 29.88 | 1002 |
| 29.87 | 1012 |
| 29.86 | 1021 |
| 29.85 | 1030 |
| 29.84 | 1039 |
| 29.83 | 1049 |
| 29.82 | 1058 |
| 29.81 | 1067 |
| 29.80 | 1076 |
| 29.79 | 1085 |
| 29.78 | 1094 |
| 29.77 | 1103 |
| 29.76 | 1113 |
| 29.75 | 1122 |
| 29.74 | 1132 |
| 29.73 | 1141 |
| 29.72 | 1150 |
| 29.71 | 1159 |
| 29.70 | 1169 |
| 29.69 | 1177 |
| 29.68 | 1186 |
| 29.67 | 1195 |
| 29.66 | 1205 |
| 29.65 | 1214 |
| 29.64 | 1224 |
| 29.63 | 1233 |
| 29.62 | 1242 |
| 29.61 | 1251 |
| 29.60 | 1260 |
| 29.59 | 1269 |
| 29.58 | 1278 |
| 29.57 | 1287 |
| 29.56 | 1296 |
| 29.55 | 1305 |
| 29.54 | 1314 |
| 29.53 | 1324 |
| 25.52 | 1333 |
| 29.51 | 1342 |
| 29.50 | 1352 |
| 29.49 | 1361 |
| 29.48 | 1370 |
| 29.47 | 1379 |
| 29.46 | 1389 |
| 29.45 | 1398 |
| 29.44 | 1408 |
| 29.43 | 1417 |
| 29.42 | 1426 |
| 29.41 | 1435 |
| 29.40 | 1445 |
| 29.39 | 1454 |
| 29.38 | 1464 |
| 29.37 | 1473 |
| 29.36 | 1482 [Pg 91] |
| 29.35 | 1491 |
| 29.34 | 1500 |
| 29.33 | 1509 |
| 29.32 | 1519 |
| 29.31 | 1528 |
| 29.30 | 1537 |
| 29.29 | 1546 |
| 29.28 | 1556 |
| 29.27 | 1565 |
| 29.26 | 1574 |
| 29.25 | 1583 |
| 29.24 | 1593 |
| 29.23 | 1603 |
| 29.22 | 1612 |
| 29.21 | 1621 |
| 29.20 | 1630 |
| 29.19 | 1639 |
| 29.18 | 1649 |
| 29.17 | 1658 |
| 29.16 | 1668 |
| 29.15 | 1677 |
| 29.14 | 1687 |
| 29.13 | 1696 |
| 29.12 | 1706 |
| 29.11 | 1715 |
| 29.10 | 1725 |
| 29.09 | 1734 |
| 29.08 | 1743 |
| 29.07 | 1752 |
| 29.06 | 1762 |
| 29.05 | 1771 |
| 29.04 | 1781 |
| 29.03 | 1790 |
| 29.02 | 1799 |
| 29.01 | 1809 |
| 29.00 | 1818 |
| 28.99 | 1827 |
| 28.98 | 1837 |
| 28.97 | 1846 |
| 28.96 | 1856 |
| 28.95 | 1865 |
| 28.94 | 1875 |
| 28.93 | 1884 |
| 28.92 | 1894 |
| 28.91 | 1903 |
| 28.90 | 1913 |
| 28.89 | 1922 |
| 28.88 | 1931 |
| 28.87 | 1941 |
| 28.86 | 1950 |
| 28.85 | 1960 |
| 28.84 | 1969 |
| 28.83 | 1979 |
| 28.82 | 1988 |
| 28.81 | 1998 |
| 28.80 | 2007 |
| 28.79 | 2016 |
| 28.78 | 2026 |
| 28.77 | 2035 |
| 28.76 | 2044 |
| 28.75 | 2054 |
| 28.74 | 2063 |
| 28.73 | 2073 |
| 28.72 | 2082 [Pg 92] |
| 28.71 | 2091 |
| 28.70 | 2101 |
| 28.69 | 2111 |
| 28.68 | 2120 |
| 28.67 | 2129 |
| 28.66 | 2139 |
| 28.65 | 2148 |
| 28.64 | 2158 |
| 28.63 | 2168 |
| 28.62 | 2177 |
| 28.61 | 2186 |
| 28.60 | 2196 |
| 28.59 | 2205 |
| 28.58 | 2215 |
| 28.57 | 2224 |
| 28.56 | 2234 |
| 28.55 | 2243 |
| 28.54 | 2253 |
| 28.53 | 2263 |
| 28.52 | 2272 |
| 28.51 | 2282 |
| 28.50 | 2291 |
| 28.49 | 2301 |
| 28.48 | 2310 |
| 28.47 | 2320 |
| 28.46 | 2329 |
| 28.45 | 2339 |
| 28.44 | 2349 |
| 28.43 | 2358 |
| 28.42 | 2368 |
| 28.41 | 2378 |
| 28.40 | 2387 |
| 28.39 | 2397 |
| 28.38 | 2407 |
| 28.37 | 2416 |
| 28.36 | 2426 |
| 28.35 | 2435 |
| 28.34 | 2445 |
| 28.33 | 2455 |
| 28.32 | 2464 |
| 28.31 | 2474 |
| 28.30 | 2483 |
| 28.29 | 2493 |
| 28.28 | 2503 |
| 28.27 | 2512 |
| 28.26 | 2522 |
| 28.25 | 2531 |
| 28.24 | 2541 |
| 28.23 | 2551 |
| 28.22 | 2561 |
| 28.21 | 2570 |
| 28.20 | 2580 |
| 28.19 | 2590 |
| 28.18 | 2600 |
| 28.17 | 2609 |
| 28.16 | 2619 |
| 28.15 | 2628 |
| 28.14 | 2638 |
| 28.13 | 2648 |
| 28.12 | 2658 |
| 28.11 | 2667 |
| 28.10 | 2677 |
| 28.09 | 2687 |
| 28.08 | 2696 [Pg 93] |
| 28.07 | 2706 |
| 28.06 | 2715 |
| 28.05 | 2726 |
| 28.04 | 2735 |
| 28.03 | 2745 |
| 28.02 | 2755 |
| 28.01 | 2765 |
| 28.00 | 2774 |
| 27.99 | 2784 |
| 27.98 | 2794 |
| 27.97 | 2804 |
| 27.96 | 2813 |
| 27.95 | 2823 |
| 27.94 | 2833 |
| 27.93 | 2843 |
| 27.92 | 2853 |
| 27.91 | 2863 |
| 27.90 | 2873 |
| 27.89 | 2882 |
| 27.88 | 2892 |
| 27.87 | 2901 |
| 27.86 | 2911 |
| 27.85 | 2921 |
| 27.84 | 2930 |
| 27.83 | 2940 |
| 27.82 | 2950 |
| 27.81 | 2960 |
| 27.80 | 2969 |
| 27.79 | 2979 |
| 27.78 | 2989 |
| 27.77 | 2999 |
| 27.76 | 3009 |
| 27.75 | 3019 |
| 27.74 | 3029 |
| 27.73 | 3039 |
| 27.72 | 3048 |
| 27.71 | 3058 |
| 27.70 | 3068 |
| 27.69 | 3078 |
| 27.68 | 3087 |
| 27.67 | 3097 |
| 27.66 | 3107 |
| 27.65 | 3117 |
| 27.64 | 3126 |
| 27.63 | 3136 |
| 27.62 | 3146 |
| 27.61 | 3156 |
| 27.60 | 3166 |
| 27.59 | 3176 |
| 27.58 | 3186 |
| 27.57 | 3196 |
| 27.56 | 3206 |
| 27.55 | 3216 |
| 27.54 | 3225 |
| 27.53 | 3235 |
| 27.52 | 3245 |
| 27.51 | 3255 |
| 27.50 | 3265 |
| 27.49 | 3275 |
| 27.48 | 3285 |
| 27.47 | 3295 |
| 27.46 | 3305 |
| 27.45 | 3315 |
| 27.44 | 3325 [Pg 94] |
| 27.43 | 3335 |
| 27.42 | 3345 |
| 27.41 | 3355 |
| 27.40 | 3365 |
| 27.39 | 3375 |
| 27.38 | 3384 |
| 27.37 | 3394 |
| 27.36 | 3404 |
| 27.35 | 3414 |
| 27.34 | 3424 |
| 27.33 | 3434 |
| 27.32 | 3444 |
| 27.31 | 3454 |
| 27.30 | 3464 |
| 27.29 | 3474 |
| 27.28 | 3484 |
| 27.27 | 3494 |
| 27.26 | 3504 |
| 27.25 | 3514 |
| 27.24 | 3524 |
| 27.23 | 3534 |
| 27.22 | 3544 |
| 27.21 | 3554 |
| 27.20 | 3564 |
| 27.19 | 3574 |
| 27.18 | 3584 |
| 27.17 | 3594 |
| 27.16 | 3604 |
| 27.15 | 3614 |
| 27.14 | 3624 |
| 27.13 | 3634 |
| 27.12 | 3644 |
| 27.11 | 3654 |
| 27.10 | 3665 |
| 27.09 | 3675 |
| 27.08 | 3685 |
| 27.07 | 3695 |
| 27.06 | 3705 |
| 27.05 | 3715 |
| 27.04 | 3725 |
| 27.03 | 3735 |
| 27.02 | 3745 |
| 27.01 | 3755 |
| 27.00 | 3765 |
| 26.99 | 3775 |
| 26.98 | 3785 |
| 26.97 | 3795 |
| 26.96 | 3806 |
| 26.95 | 3816 |
| 26.94 | 3826 |
| 26.93 | 3836 |
| 26.92 | 3846 |
| 26.91 | 3856 |
| 26.90 | 3866 |
| 26.89 | 3876 |
| 26.88 | 3886 |
| 26.87 | 3897 |
| 26.86 | 3907 |
| 26.85 | 3917 |
| 26.84 | 3927 |
| 26.83 | 3938 |
| 26.82 | 3948 |
| 26.81 | 3958 |
| 26.80 | 3968 [Pg 95] |
| 26.79 | 3978 |
| 26.78 | 3988 |
| 26.77 | 3999 |
| 26.76 | 4009 |
| 26.75 | 4019 |
| 26.74 | 4030 |
| 26.73 | 4040 |
| 26.72 | 4050 |
| 26.71 | 4060 |
| 26.70 | 4070 |
| 26.69 | 4081 |
| 26.68 | 4091 |
| 26.67 | 4101 |
| 26.66 | 4111 |
| 26.65 | 4122 |
| 26.64 | 4132 |
| 26.63 | 4142 |
| 26.62 | 4152 |
| 26.61 | 4163 |
| 26.60 | 4173 |
| 26.59 | 4183 |
| 26.58 | 4193 |
| 26.57 | 4203 |
| 26.56 | 4213 |
| 26.55 | 4223 |
| 26.54 | 4233 |
| 26.53 | 4244 |
| 26.52 | 4254 |
| 26.51 | 4264 |
| 26.50 | 4274 |
| 26.49 | 4284 |
| 26.48 | 4294 |
| 26.47 | 4304 |
| 26.46 | 4315 |
| 26.45 | 4326 |
| 26.44 | 4336 |
| 26.43 | 4347 |
| 26.42 | 4357 |
| 26.41 | 4368 |
| 26.40 | 4378 |
| 26.39 | 4388 |
| 26.38 | 4399 |
| 26.37 | 4409 |
| 26.36 | 4419 |
| 26.35 | 4430 |
| 26.34 | 4440 |
| 26.33 | 4450 |
| 26.32 | 4461 |
| 26.31 | 4472 |
| 26.30 | 4482 |
| 26.29 | 4492 |
| 26.28 | 4502 |
| 26.27 | 4513 |
| 26.26 | 4523 |
| 26.25 | 4533 |
| 26.24 | 4544 |
| 26.23 | 4554 |
| 26.22 | 4565 |
| 26.21 | 4575 |
| 26.20 | 4585 |
| 26.19 | 4596 |
| 26.18 | 4606 |
| 26.17 | 4617 |
| 26.16 | 4627 [Pg 96] |
| 26.15 | 4638 |
| 26.14 | 4648 |
| 26.13 | 4658 |
| 26.12 | 4669 |
| 26.11 | 4679 |
| 26.10 | 4690 |
| 26.09 | 4700 |
| 26.08 | 4711 |
| 26.07 | 4721 |
| 26.06 | 4731 |
| 26.05 | 4742 |
| 26.04 | 4752 |
| 26.03 | 4763 |
| 26.02 | 4773 |
| 26.01 | 4784 |
| 26.00 | 4794 |
| 25.99 | 4805 |
| 25.98 | 4815 |
| 25.97 | 4826 |
| 25.96 | 4836 |
| 25.95 | 4847 |
| 25.94 | 4857 |
| 25.93 | 4868 |
| 25.92 | 4878 |
| 25.91 | 4889 |
| 25.90 | 4899 |
| 25.89 | 4910 |
| 25.88 | 4920 |
| 25.87 | 4931 |
| 25.86 | 4941 |
| 25.85 | 4952 |
| 25.84 | 4962 |
| 25.83 | 4973 |
| 25.82 | 4983 |
| 25.81 | 4994 |
| 25.80 | 5004 |
| 25.79 | 5014 |
| 25.78 | 5025 |
| 25.77 | 5036 |
| 25.76 | 5046 |
| 25.75 | 5057 |
| 25.74 | 5067 |
| 25.73 | 5078 |
| 25.72 | 5088 |
| 25.71 | 5099 |
| 25.70 | 5110 |
| 25.69 | 5121 |
| 25.68 | 5132 |
| 25.67 | 5142 |
| 25.66 | 5153 |
| 25.65 | 5164 |
| 25.64 | 5174 |
| 25.63 | 5185 |
| 20.62 | 5195 |
| 25.61 | 5206 |
| 25.60 | 5216 |
| 25.59 | 5227 |
| 25.58 | 5237 |
| 25.57 | 5248 |
| 25.56 | 5259 |
| 25.55 | 5270 |
| 25.54 | 5281 |
| 25.53 | 5291 |
| 25.52 | 5302 [Pg 97] |
| 25.51 | 5312 |
| 25.50 | 5323 |
| 25.49 | 5333 |
| 25.48 | 5344 |
| 25.47 | 5355 |
| 25.46 | 5365 |
| 25.45 | 5376 |
| 25.44 | 5387 |
| 25.43 | 5397 |
| 25.42 | 5408 |
| 25.41 | 5419 |
| 25.40 | 5429 |
| 25.39 | 5440 |
| 25.38 | 5451 |
| 25.37 | 5462 |
| 25.36 | 5473 |
| 25.35 | 5483 |
| 25.34 | 5494 |
| 25.33 | 5505 |
| 25.32 | 5516 |
| 25.31 | 5527 |
| 25.30 | 5537 |
| 25.29 | 5548 |
| 25.28 | 5559 |
| 25.27 | 5570 |
| 25.26 | 5581 |
| 25.25 | 5592 |
| 25.24 | 5602 |
| 25.23 | 5613 |
| 25.22 | 5624 |
| 25.21 | 5635 |
| 25.20 | 5646 |
| 25.19 | 5657 |
| 25.18 | 5668 |
| 25.17 | 5679 |
| 25.16 | 5689 |
| 25.15 | 5700 |
| 25.14 | 5711 |
| 25.13 | 5722 |
| 25.12 | 5733 |
| 25.11 | 5744 |
| 25.10 | 5754 |
| 25.09 | 5765 |
| 25.08 | 5776 |
| 25.07 | 5787 |
| 25.06 | 5798 |
| 25.05 | 5809 |
| 25.04 | 5820 |
| 25.03 | 5831 |
| 25.02 | 5842 |
| 25.01 | 5853 |
| 25.00 | 5863 |
| 24.99 | 5874 |
| 24.98 | 5885 |
| 24.97 | 5896 |
| 24.96 | 5907 |
| 24.95 | 5918 |
| 24.94 | 5929 |
| 24.93 | 5940 |
| 24.92 | 5950 |
| 24.91 | 5962 |
| 24.90 | 5972 |
| 24.89 | 5983 |
| 24.88 | 5994 [Pg 98] |
| 24.87 | 6005 |
| 24.86 | 6016 |
| 24.85 | 6027 |
| 24.84 | 6038 |
| 24.83 | 6049 |
| 24.82 | 6060 |
| 24.81 | 6071 |
| 24.80 | 6082 |
| 24.79 | 6093 |
| 24.78 | 6104 |
| 24.77 | 6115 |
| 24.76 | 6126 |
| 24.75 | 6137 |
| 24.74 | 6148 |
| 24.73 | 6159 |
| 24.72 | 6170 |
| 24.71 | 6181 |
| 24.70 | 6192 |
| 24.69 | 6203 |
| 24.68 | 6214 |
| 24.67 | 6225 |
| 24.66 | 6236 |
| 24.65 | 6247 |
| 24.64 | 6258 |
| 24.63 | 6269 |
| 24.62 | 6280 |
| 24.61 | 6291 |
| 24.60 | 6302 |
| 24.59 | 6313 |
| 24.58 | 6324 |
| 24.57 | 6335 |
| 24.56 | 6346 |
| 24.55 | 6357 |
| 24.54 | 6368 |
| 24.53 | 6379 |
| 24.52 | 6390 |
| 24.51 | 6401 |
| 24.50 | 6412 |
| 24.49 | 6424 |
| 24.48 | 6435 |
| 24.47 | 6446 |
| 24.46 | 6458 |
| 24.45 | 6469 |
| 24.44 | 6480 |
| 24.43 | 6491 |
| 24.42 | 6503 |
| 24.41 | 6514 |
| 24.40 | 6525 |
| 24.39 | 6536 |
| 24.38 | 6547 |
| 24.37 | 6559 |
| 24.36 | 6570 |
| 24.35 | 6581 |
| 24.34 | 6592 |
| 24.33 | 6603 |
| 24.32 | 6615 |
| 24.31 | 6626 |
| 24.30 | 6637 |
| 24.29 | 6648 |
| 24.28 | 6659 |
| 24.27 | 6671 |
| 24.26 | 6682 |
| 24.25 | 6693 |
| 24.24 | 6705 [Pg 99] |
| 24.23 | 6716 |
| 24.22 | 6727 |
| 24.21 | 6738 |
| 24.20 | 6750 |
| 24.19 | 6761 |
| 24.18 | 6772 |
| 24.17 | 6783 |
| 24.16 | 6795 |
| 24.15 | 6806 |
| 24.14 | 6817 |
| 24.13 | 6828 |
| 24.12 | 6840 |
| 24.11 | 6851 |
| 24.10 | 6862 |
| 24.09 | 6873 |
| 24.08 | 6885 |
| 24.07 | 6896 |
| 24.06 | 6907 |
| 24.05 | 6919 |
| 24.04 | 6930 |
| 24.03 | 6941 |
| 24.02 | 6953 |
| 24.01 | 6964 |
| 24.00 | 6976 |
| 23.99 | 6987 |
| 23.98 | 6999 |
| 23.97 | 7010 |
| 23.96 | 7022 |
| 23.95 | 7033 |
| 23.94 | 7045 |
| 23.93 | 7056 |
| 23.92 | 7068 |
| 23.91 | 7079 |
| 23.90 | 7090 |
| 23.89 | 7101 |
| 23.88 | 7113 |
| 23.87 | 7124 |
| 23.86 | 7135 |
| 23.85 | 7146 |
| 23.84 | 7157 |
| 23.83 | 7168 |
| 23.82 | 7180 |
| 23.81 | 7191 |
| 23.80 | 7203 |
| 23.79 | 7214 |
| 23.78 | 7226 |
| 23.77 | 7237 |
| 23.76 | 7249 |
| 23.75 | 7261 |
| 23.74 | 7272 |
| 23.73 | 7283 |
| 23.72 | 7294 |
| 23.71 | 7305 |
| 23.70 | 7316 |
| 23.69 | 7327 |
| 23.68 | 7339 |
| 23.67 | 7350 |
| 23.66 | 7362 |
| 23.65 | 7374 |
| 23.64 | 7386 |
| 23.63 | 7398 |
| 23.62 | 7409 |
| 23.61 | 7421 |
| 23.60 | 7433 [Pg 100] |
| 23.59 | 7445 |
| 23.58 | 7456 |
| 23.57 | 7468 |
| 23.56 | 7480 |
| 23.55 | 7492 |
| 23.54 | 7503 |
| 23.53 | 7515 |
| 23.52 | 7527 |
| 23.51 | 7539 |
| 23.50 | 7550 |
| 23.49 | 7562 |
| 23.48 | 7574 |
| 23.47 | 7585 |
| 23.46 | 7597 |
| 23.45 | 7609 |
| 23.44 | 7621 |
| 23.43 | 7633 |
| 23.42 | 7644 |
| 23.41 | 7656 |
| 23.40 | 7667 |
| 23.39 | 7679 |
| 23.38 | 7690 |
| 23.37 | 7702 |
| 23.36 | 7713 |
| 23.35 | 7725 |
| 23.34 | 7736 |
| 23.33 | 7748 |
| 23.32 | 7759 |
| 23.31 | 7771 |
| 23.30 | 7782 |
| 23.29 | 7793 |
| 23.28 | 7805 |
| 23.27 | 7817 |
| 23.26 | 7829 |
| 23.25 | 7841 |
| 23.24 | 7853 |
| 23.23 | 7865 |
| 23.22 | 7876 |
| 23.21 | 7888 |
| 23.20 | 7900 |
| 23.19 | 7912 |
| 23.18 | 7923 |
| 23.17 | 7935 |
| 23.16 | 7946 |
| 23.15 | 7958 |
| 23.14 | 7969 |
| 23.13 | 7981 |
| 23.12 | 7092 |
| 23.11 | 8004 |
| 23.10 | 8015 |
| 23.09 | 8027 |
| 23.08 | 8039 |
| 23.07 | 8051 |
| 23.06 | 8063 |
| 23.05 | 8075 |
| 23.04 | 8086 |
| 23.03 | 8098 |
| 23.02 | 8110 |
| 23.01 | 8122 |
| 23.00 | 8134 |
| 22.99 | 8146 |
| 22.98 | 8158 |
| 22.97 | 8170 |
| 22.96 | 8182 [Pg 101] |
| 22.95 | 8194 |
| 22.94 | 8206 |
| 22.93 | 8218 |
| 22.92 | 8230 |
| 22.91 | 8242 |
| 22.90 | 8254 |
| 22.89 | 8266 |
| 22.88 | 8278 |
| 22.87 | 8290 |
| 22.86 | 8302 |
| 22.85 | 8314 |
| 22.84 | 8326 |
| 22.83 | 8338 |
| 22.82 | 8850 |
| 22.81 | 8362 |
| 22.80 | 8374 |
| 22.79 | 8386 |
| 22.78 | 8398 |
| 22.77 | 8410 |
| 22.76 | 8422 |
| 22.75 | 8434 |
| 22.74 | 8446 |
| 22.73 | 8458 |
| 22.72 | 8470 |
| 22.71 | 8482 |
| 22.70 | 8495 |
| 22.69 | 8507 |
| 22.68 | 8519 |
| 22.67 | 8531 |
| 22.66 | 8543 |
| 22.65 | 8555 |
| 22.64 | 8567 |
| 22.63 | 8579 |
| 22.62 | 8591 |
| 22.61 | 8603 |
| 22.60 | 8615 |
| 22.59 | 8627 |
| 22.58 | 8638 |
| 22.57 | 8650 |
| 22.56 | 8661 |
| 22.55 | 8673 |
| 22.54 | 8685 |
| 22.53 | 8697 |
| 22.52 | 8709 |
| 22.51 | 8721 |
| 22.50 | 8733 |
| 22.49 | 8745 |
| 22.48 | 8757 |
| 22.47 | 8769 |
| 22.46 | 8781 |
| 22.45 | 8793 |
| 22.44 | 8806 |
| 22.43 | 8818 |
| 22.42 | 8830 |
| 22.41 | 8842 |
| 22.40 | 8855 |
| 22.39 | 8867 |
| 22.38 | 8879 |
| 22.37 | 8891 |
| 22.36 | 8904 |
| 22.35 | 8916 |
| 22.34 | 8928 |
| 22.33 | 8941 |
| 22.32 | 8953 [Pg 102] |
| 22.31 | 8965 |
| 22.30 | 8977 |
| 22.29 | 8090 |
| 22.28 | 9002 |
| 22.27 | 9014 |
| 22.26 | 9026 |
| 22.25 | 9039 |
| 22.24 | 9051 |
| 22.23 | 9063 |
| 22.22 | 9075 |
| 22.21 | 9088 |
| 22.20 | 9100 |
| 22.19 | 9113 |
| 22.18 | 9125 |
| 22.17 | 9138 |
| 22.16 | 9150 |
| 22.15 | 9162 |
| 22.14 | 9174 |
| 22.13 | 9187 |
| 22.12 | 9199 |
| 22.11 | 9212 |
| 22.10 | 9224 |
| 22.09 | 9236 |
| 22.08 | 9249 |
| 22.07 | 9262 |
| 22.06 | 9274 |
| 22.05 | 9286 |
| 22.04 | 9298 |
| 22.03 | 9311 |
| 22.02 | 9323 |
| 22.01 | 9336 |
| 22.00 | 9348 |
| 21.99 | 9360 |
| 21.98 | 9372 |
| 21.97 | 9384 |
| 21.96 | 9397 |
| 21.95 | 9410 |
| 21.94 | 9422 |
| 21.93 | 9435 |
| 21.92 | 9447 |
| 21.91 | 9460 |
| 21.90 | 9472 |
| 21.89 | 9485 |
| 21.88 | 9497 |
| 21.87 | 9510 |
| 21.86 | 9522 |
| 21.85 | 9535 |
| 21.84 | 9547 |
| 21.83 | 9560 |
| 21.82 | 9572 |
| 21.81 | 9585 |
| 21.80 | 9597 |
| 21.79 | 9610 |
| 21.78 | 9622 |
| 21.77 | 9635 |
| 21.76 | 9647 |
| 21.75 | 9660 |
| 21.74 | 9672 |
| 21.73 | 9685 |
| 21.72 | 9697 |
| 21.71 | 9710 |
| 21.70 | 9722 |
| 21.69 | 9735 |
| 21.68 | 9747 [Pg 103] |
| 21.67 | 9760 |
| 21.66 | 9772 |
| 21.65 | 9785 |
| 21.64 | 9797 |
| 21.63 | 9810 |
| 21.62 | 9822 |
| 21.61 | 9835 |
| 21.60 | 9848 |
| 21.59 | 9861 |
| 21.58 | 9873 |
| 21.57 | 9886 |
| 21.56 | 9898 |
| 21.55 | 9911 |
| 21.54 | 9923 |
| 21.53 | 9936 |
| 21.52 | 9949 |
| 21.51 | 9962 |
| 21.50 | 9974 |
| 21.49 | 9987 |
| 21.48 | 9999 |
| 21.47 | 10012 |
| 21.46 | 10025 |
| 21.45 | 10038 |
| 21.44 | 10050 |
| 21.43 | 10063 |
| 21.42 | 10075 |
| 21.41 | 10088 |
| 21.40 | 10101 |
| 21.39 | 10114 |
| 21.38 | 10126 |
| 21.37 | 10139 |
| 21.36 | 10151 |
| 21.35 | 10164 |
| 21.34 | 10176 |
| 21.33 | 10189 |
| 21.32 | 10202 |
| 21.31 | 10214 |
| 21.30 | 10228 |
| 21.29 | 10241 |
| 21.28 | 10253 |
| 21.27 | 10266 |
| 21.26 | 10278 |
| 21.25 | 10291 |
| 21.24 | 10304 |
| 21.23 | 10317 |
| 21.22 | 10330 |
| 21.21 | 10343 |
| 21.20 | 10355 |
| 21.19 | 10368 |
| 21.18 | 10381 |
| 21.17 | 10394 |
| 21.16 | 10407 |
| 21.15 | 10420 |
| 21.14 | 10432 |
| 21.13 | 10445 |
| 21.12 | 10458 |
| 21.11 | 10471 |
| 21.10 | 10484 |
| 21.09 | 10497 |
| 21.08 | 10509 |
| 21.07 | 10522 |
| 21.06 | 10535 |
| 21.05 | 10548 |
| 21.04 | 10561 [Pg 104] |
| 21.03 | 10574 |
| 21.02 | 10587 |
| 21.01 | 10600 |
| 21.00 | 10613 |
| 20.99 | 10627 |
| 20.98 | 10640 |
| 20.97 | 10654 |
| 20.96 | 10667 |
| 20.95 | 10681 |
| 20.94 | 10694 |
| 20.93 | 10707 |
| 20.92 | 10720 |
| 20.91 | 10733 |
| 20.90 | 10746 |
| 20.89 | 10759 |
| 20.88 | 10772 |
| 20.87 | 10785 |
| 20.86 | 10798 |
| 20.85 | 10811 |
| 20.84 | 10824 |
| 20.83 | 10837 |
| 20.82 | 10850 |
| 20.81 | 10863 |
| 20.80 | 10876 |
| 20.79 | 10889 |
| 20.78 | 10902 |
| 20.77 | 10915 |
| 20.76 | 10928 |
| 20.75 | 10941 |
| 20.74 | 10954 |
| 20.73 | 10967 |
| 20.72 | 10980 |
| 20.71 | 10993 |
| 20.70 | 11006 |
| 20.69 | 11019 |
| 20.68 | 11032 |
| 20.67 | 11045 |
| 20.66 | 11058 |
| 20.65 | 11071 |
| 20.64 | 11084 |
| 20.63 | 11097 |
| 20.62 | 11110 |
| 20.61 | 11123 |
| 20.60 | 11136 |
| 20.59 | 11149 |
| 20.58 | 11163 |
| 20.57 | 11176 |
| 20.56 | 11190 |
| 20.55 | 11204 |
| 20.54 | 11217 |
| 20.53 | 11230 |
| 20.52 | 11243 |
| 20.51 | 11257 |
| 20.50 | 11270 |
| 20.49 | 11284 |
| 20.48 | 11297 |
| 20.47 | 11311 |
| 20.46 | 11324 |
| 20.45 | 11338 |
| 20.44 | 11351 |
| 20.43 | 11364 |
| 20.42 | 11377 |
| 20.41 | 11391 |
| 20.40 | 11404 [Pg 105] |
| 20.39 | 11418 |
| 20.38 | 11431 |
| 20.37 | 11444 |
| 20.36 | 11457 |
| 20.35 | 11470 |
| 20.34 | 11483 |
| 20.33 | 11496 |
| 20.32 | 11509 |
| 20.31 | 11523 |
| 20.30 | 11536 |
| 20.29 | 11550 |
| 20.28 | 11563 |
| 20.27 | 11577 |
| 20.26 | 11591 |
| 20.25 | 11605 |
| 20.24 | 11618 |
| 20.23 | 11632 |
| 20.22 | 11645 |
| 20.21 | 11659 |
| 20.20 | 11673 |
| 20.19 | 11687 |
| 20.18 | 11700 |
| 20.17 | 11714 |
| 20.16 | 11727 |
| 20.15 | 11741 |
| 20.14 | 11754 |
| 20.13 | 11768 |
| 20.12 | 11781 |
| 20.11 | 11795 |
| 20.10 | 11808 |
| 20.09 | 11821 |
| 20.08 | 11835 |
| 20.07 | 11859 |
| 20.06 | 11863 |
| 20.05 | 11877 |
| 20.04 | 11891 |
| 20.03 | 11905 |
| 20.02 | 11918 |
| 20.01 | 11932 |
| 20.00 | 11945 |
[Pg 106]
The following table is to be used when applying the modified formula of chapter II:
Rule.—Find
in the table the logarithms of the barometer readings to hundredths
of an inch. Subtract these logarithms and multiply the remainder by
60000. The product is the approximate difference in altitude between
the two stations. To apply the corrections for temperature, add the
temperatures of the two stations and subtract 60°. Increase the above
approximate value by of itself for each degree of
excess above 60°. If the sum of the temperature is less than 60°
diminish the value by a like amount.
[Pg 107]
| Bar. Height. |
Log. |
| 2200 | 3.34242 |
| 01 | .34262 |
| 02 | .34282 |
| 03 | .34301 |
| 04 | .34321 |
| 05 | .34341 |
| 06 | .34361 |
| 07 | .34380 |
| 08 | .34400 |
| 09 | .34420 |
| 10 | .34439 |
| 11 | .34459 |
| 12 | .34479 |
| 13 | .34498 |
| 14 | .34518 |
| 15 | .34537 |
| 16 | .34557 |
| 17 | .34577 |
| 18 | .34596 |
| 19 | .34616 |
| 20 | .34635 |
| 21 | .34655 |
| 22 | .34674 |
| 23 | .34694 |
| 24 | .34713 |
| 25 | .34733 |
| 26 | .34753 |
| 27 | .34772 |
| 28 | .34792 |
| 29 | .34811 |
| 30 | .34830 |
| 31 | .34850 |
| 32 | .34869 |
| 33 | .34889 |
| 34 | .34908 |
| 35 | .34928 |
| 36 | .34947 |
| 37 | .34967 |
| 38 | .34986 |
| 39 | .35005 |
| 40 | .35025 |
| 41 | .35044 |
| 42 | .35064 |
| 43 | .35083 |
| 44 | .35102 |
| 45 | .35122 |
| 46 | .35141 |
| 47 | .35160 |
| 48 | .35180 |
| 49 | .35199 |
| 50 | .35218 |
| 51 | .35238 |
| 52 | .35257 |
| 53 | .35276 |
| 54 | .35295 |
| 55 | .35315 |
| 56 | .35334 |
| 57 | .35353 |
| 58 | .35372 |
| 59 | .35392 |
| 60 | .35411 [Pg 108] |
| 61 | .35430 |
| 62 | .35449 |
| 63 | .35468 |
| 64 | .35488 |
| 65 | .35507 |
| 66 | .35526 |
| 67 | .35545 |
| 68 | .35564 |
| 69 | .35583 |
| 70 | .35603 |
| 71 | .35622 |
| 72 | .35641 |
| 73 | .35660 |
| 74 | .35679 |
| 75 | .35698 |
| 76 | .35717 |
| 77 | .35736 |
| 78 | .35755 |
| 79 | .35774 |
| 80 | .35793 |
| 81 | .35813 |
| 82 | .35832 |
| 83 | .35851 |
| 84 | .35870 |
| 85 | .35889 |
| 86 | .35908 |
| 87 | .35927 |
| 88 | .35946 |
| 89 | .35965 |
| 90 | .35984 |
| 91 | .36003 |
| 92 | .36021 |
| 93 | .36040 |
| 94 | .36059 |
| 95 | .36078 |
| 96 | .36097 |
| 97 | .36116 |
| 98 | .36135 |
| 99 | .36154 |
| 2300 | 3.36173 |
| 01 | .36192 |
| 02 | .36211 |
| 03 | .36229 |
| 04 | .36248 |
| 05 | .36267 |
| 06 | .36286 |
| 07 | .36305 |
| 08 | .36324 |
| 09 | .36342 |
| 10 | .36361 |
| 11 | .36380 |
| 12 | .36399 |
| 13 | .36418 |
| 14 | .36436 |
| 15 | .36455 |
| 16 | .36474 |
| 17 | .36493 |
| 18 | .36511 |
| 19 | .36530 |
| 20 | .36549 |
| 21 | .36568 |
| 22 | .36586 |
| 23 | .36605 |
| 24 | .36624 |
| 25 | .36642 |
| 26 | .36661 [Pg 109] |
| 27 | .36680 |
| 28 | .36698 |
| 29 | .36717 |
| 30 | .36736 |
| 31 | .36754 |
| 32 | .36773 |
| 33 | .36791 |
| 34 | .36810 |
| 35 | .36829 |
| 36 | .36847 |
| 37 | .36866 |
| 38 | .36884 |
| 39 | .36903 |
| 40 | .36922 |
| 41 | .36940 |
| 42 | .36959 |
| 43 | .36977 |
| 44 | .36996 |
| 45 | .37014 |
| 46 | .37033 |
| 47 | .37051 |
| 48 | .37070 |
| 49 | .37088 |
| 50 | .37107 |
| 51 | .37125 |
| 52 | .37144 |
| 53 | .37162 |
| 54 | .37181 |
| 55 | .37199 |
| 56 | .37218 |
| 57 | .37236 |
| 58 | .37254 |
| 59 | .37273 |
| 60 | .37291 |
| 61 | .37310 |
| 62 | .37328 |
| 63 | .37346 |
| 64 | .37365 |
| 65 | .37383 |
| 66 | .37401 |
| 67 | .37420 |
| 68 | .37438 |
| 69 | .37457 |
| 70 | .37475 |
| 71 | .37493 |
| 72 | .37511 |
| 73 | .37530 |
| 74 | .37548 |
| 75 | .37566 |
| 76 | .37585 |
| 77 | .37603 |
| 78 | .37621 |
| 79 | .37639 |
| 80 | .37658 |
| 81 | .37676 |
| 82 | .37694 |
| 83 | .37712 |
| 84 | .37731 |
| 85 | .37749 |
| 86 | .37767 |
| 87 | .37785 |
| 88 | .37803 |
| 89 | .37822 |
| 90 | .37840 |
| 91 | .37858 |
| 92 | .37876 [Pg 110] |
| 93 | .37894 |
| 94 | .37912 |
| 95 | .37931 |
| 96 | .37949 |
| 97 | .37967 |
| 98 | .37985 |
| 99 | .38003 |
| 2400 | 3.38021 |
| 01 | .38039 |
| 02 | .38057 |
| 03 | .38075 |
| 04 | .38093 |
| 05 | .38112 |
| 06 | .38130 |
| 07 | .38148 |
| 08 | .38166 |
| 09 | .38184 |
| 10 | .38202 |
| 11 | .38220 |
| 12 | .38238 |
| 13 | .38256 |
| 14 | .38274 |
| 15 | .38292 |
| 16 | .38310 |
| 17 | .38328 |
| 18 | .38346 |
| 19 | .38364 |
| 20 | .38382 |
| 21 | .38399 |
| 22 | .38417 |
| 23 | .38435 |
| 24 | .38453 |
| 25 | .38471 |
| 26 | .38489 |
| 27 | .38507 |
| 28 | .38525 |
| 29 | .38543 |
| 30 | .38561 |
| 31 | .38579 |
| 32 | .38596 |
| 33 | .38614 |
| 34 | .38632 |
| 35 | .38650 |
| 36 | .38668 |
| 37 | .38686 |
| 38 | .38703 |
| 39 | .38721 |
| 40 | .38739 |
| 41 | .38757 |
| 42 | .38775 |
| 43 | .38792 |
| 44 | .38810 |
| 45 | .38828 |
| 46 | .38846 |
| 47 | .38863 |
| 48 | .38881 |
| 49 | .38899 |
| 50 | .38917 |
| 51 | .38934 |
| 52 | .38952 |
| 53 | .38970 |
| 54 | .38987 |
| 55 | .39005 |
| 56 | .39023 |
| 57 | .39041 |
| 58 | .39058 [Pg 111] |
| 59 | .39076 |
| 60 | .39094 |
| 61 | .39111 |
| 62 | .39129 |
| 63 | .39146 |
| 64 | .39164 |
| 65 | .39182 |
| 66 | .39199 |
| 67 | .39217 |
| 68 | .39235 |
| 69 | .39252 |
| 70 | .39270 |
| 71 | .39287 |
| 72 | .39305 |
| 73 | .39322 |
| 74 | .39340 |
| 75 | .39358 |
| 76 | .39375 |
| 77 | .39393 |
| 78 | .39410 |
| 79 | .39428 |
| 80 | .39445 |
| 81 | .39463 |
| 82 | .39480 |
| 83 | .39498 |
| 84 | .39515 |
| 85 | .39533 |
| 86 | .39550 |
| 87 | .39568 |
| 88 | .39585 |
| 89 | .39602 |
| 90 | .39620 |
| 91 | .39637 |
| 92 | .39655 |
| 94 | .39672 |
| 94 | .39690 |
| 95 | .39707 |
| 96 | .39724 |
| 97 | .39742 |
| 98 | .39759 |
| 99 | .39777 |
| 2500 | 3.39794 |
| 01 | .39811 |
| 02 | .39829 |
| 03 | .39846 |
| 04 | .39863 |
| 05 | .39881 |
| 06 | .39898 |
| 07 | .39915 |
| 08 | .39933 |
| 09 | .39950 |
| 10 | .39967 |
| 11 | .39985 |
| 12 | .40002 |
| 13 | .40019 |
| 14 | .40037 |
| 15 | .40054 |
| 16 | .40071 |
| 17 | .40088 |
| 18 | .40106 |
| 19 | .40123 |
| 20 | .40140 |
| 21 | .40157 |
| 22 | .40175 |
| 23 | .40192 |
| 24 | .40209 [Pg 112] |
| 25 | .40226 |
| 26 | .40243 |
| 27 | .40261 |
| 28 | .40278 |
| 29 | .40295 |
| 30 | .40312 |
| 31 | .40329 |
| 32 | .40346 |
| 33 | .40364 |
| 34 | .40381 |
| 35 | .40398 |
| 36 | .40415 |
| 37 | .40432 |
| 38 | .40449 |
| 39 | .40466 |
| 40 | .40483 |
| 41 | .40500 |
| 42 | .40518 |
| 43 | .40535 |
| 44 | .40552 |
| 45 | .40569 |
| 46 | .40586 |
| 47 | .40603 |
| 48 | .40620 |
| 49 | .40637 |
| 50 | .40654 |
| 51 | .40671 |
| 52 | .40688 |
| 53 | .40705 |
| 54 | .40722 |
| 55 | .40739 |
| 56 | .40756 |
| 57 | .40773 |
| 58 | .40790 |
| 59 | .40807 |
| 60 | .40824 |
| 61 | .40841 |
| 62 | .40858 |
| 63 | .40875 |
| 64 | .40892 |
| 65 | .40909 |
| 66 | .40926 |
| 67 | .40943 |
| 68 | .40960 |
| 69 | .40976 |
| 70 | .40993 |
| 71 | .41010 |
| 72 | .41027 |
| 73 | .41044 |
| 74 | .41061 |
| 75 | .41078 |
| 76 | .41095 |
| 77 | .41111 |
| 78 | .41128 |
| 79 | .41145 |
| 80 | .41162 |
| 81 | .41179 |
| 82 | .41196 |
| 83 | .41212 |
| 84 | .41229 |
| 85 | .41246 |
| 86 | .41263 |
| 87 | .41280 |
| 88 | .41296 |
| 89 | .41313 |
| 90 | .41330 [Pg 113] |
| 91 | .41347 |
| 92 | .41364 |
| 93 | .41380 |
| 94 | .41397 |
| 95 | .41414 |
| 96 | .41430 |
| 97 | .41447 |
| 98 | .41464 |
| 99 | .41481 |
| 2600 | 3.41497 |
| 01 | .41514 |
| 02 | .41531 |
| 03 | .41547 |
| 04 | .41564 |
| 05 | .41581 |
| 06 | .41597 |
| 07 | .41614 |
| 08 | .41631 |
| 09 | .41647 |
| 10 | .41664 |
| 11 | .41681 |
| 12 | .41697 |
| 13 | .41713 |
| 14 | .41731 |
| 15 | .41747 |
| 16 | .41764 |
| 17 | .41781 |
| 18 | .41797 |
| 19 | .41814 |
| 20 | .41831 |
| 21 | .41847 |
| 22 | .41863 |
| 23 | .41880 |
| 24 | .41896 |
| 25 | .41913 |
| 26 | .41929 |
| 27 | .41946 |
| 28 | .41963 |
| 29 | .41979 |
| 30 | .41996 |
| 31 | .42012 |
| 32 | .42029 |
| 33 | .42045 |
| 34 | .42062 |
| 35 | .42078 |
| 36 | .42095 |
| 37 | .42111 |
| 38 | .42127 |
| 39 | .42144 |
| 40 | .42160 |
| 41 | .42177 |
| 42 | .42193 |
| 43 | .42210 |
| 44 | .42226 |
| 45 | .42243 |
| 46 | .42259 |
| 47 | .42275 |
| 48 | .42292 |
| 49 | .42308 |
| 50 | .42325 |
| 51 | .42341 |
| 52 | .42357 |
| 53 | .42374 |
| 54 | .42390 |
| 55 | .42406 |
| 56 | .42423 [Pg 114] |
| 57 | .42439 |
| 58 | .42455 |
| 59 | .42472 |
| 60 | .42488 |
| 61 | .42504 |
| 62 | .42521 |
| 63 | .42537 |
| 64 | .42553 |
| 65 | .42570 |
| 66 | .42586 |
| 67 | .42602 |
| 68 | .42619 |
| 69 | .42635 |
| 70 | .42651 |
| 71 | .42667 |
| 72 | .42684 |
| 73 | .42700 |
| 74 | .42716 |
| 75 | .42732 |
| 76 | .42749 |
| 77 | .42765 |
| 78 | .42781 |
| 79 | .42797 |
| 80 | .42813 |
| 81 | .42830 |
| 82 | .42846 |
| 83 | .42862 |
| 84 | .42878 |
| 85 | .42894 |
| 86 | .42911 |
| 87 | .42927 |
| 88 | .42943 |
| 89 | .42959 |
| 90 | .42975 |
| 91 | .42991 |
| 92 | .43008 |
| 93 | .43024 |
| 94 | .43040 |
| 95 | .43056 |
| 96 | .43072 |
| 97 | .43088 |
| 98 | .43104 |
| 99 | .43120 |
| 2700 | 3.43136 |
| 01 | .43152 |
| 02 | .43169 |
| 03 | .43185 |
| 04 | .43201 |
| 05 | .43217 |
| 06 | .43233 |
| 07 | .43249 |
| 08 | .43265 |
| 09 | .43281 |
| 10 | .43297 |
| 11 | .43313 |
| 12 | .43329 |
| 13 | .43345 |
| 14 | .43361 |
| 15 | .43377 |
| 16 | .43393 |
| 17 | .43409 |
| 18 | .43425 |
| 19 | .43441 |
| 20 | .43457 |
| 21 | .43473 |
| 22 | .43489 [Pg 115] |
| 23 | .43505 |
| 24 | .43521 |
| 25 | .43537 |
| 26 | .43553 |
| 27 | .43569 |
| 28 | .43584 |
| 29 | .43600 |
| 30 | .43616 |
| 31 | .43632 |
| 32 | .43648 |
| 33 | .43664 |
| 34 | .43680 |
| 35 | .43696 |
| 36 | .43712 |
| 37 | .43727 |
| 38 | .43743 |
| 39 | .43759 |
| 40 | .43775 |
| 41 | .43791 |
| 42 | .43807 |
| 43 | .48823 |
| 44 | .43838 |
| 45 | .43854 |
| 46 | .43870 |
| 47 | .43886 |
| 48 | .43902 |
| 49 | .43917 |
| 50 | .43933 |
| 51 | .43949 |
| 52 | .43965 |
| 53 | .43981 |
| 54 | .43996 |
| 55 | .44012 |
| 56 | .44028 |
| 57 | .44044 |
| 58 | .44059 |
| 59 | .44075 |
| 60 | .44091 |
| 61 | .44107 |
| 62 | .44122 |
| 63 | .44138 |
| 64 | .44154 |
| 65 | .44170 |
| 66 | .44185 |
| 67 | .44201 |
| 68 | .44217 |
| 69 | .44232 |
| 70 | .44248 |
| 71 | .44264 |
| 72 | .44279 |
| 73 | .44295 |
| 74 | .44311 |
| 75 | .44326 |
| 76 | .44342 |
| 77 | .44358 |
| 78 | .44373 |
| 79 | .44389 |
| 80 | .44404 |
| 81 | .44420 |
| 82 | .44436 |
| 83 | .44451 |
| 84 | .44467 |
| 85 | .44483 |
| 86 | .44498 |
| 87 | .44514 |
| 88 | .44529 [Pg 116] |
| 89 | .44545 |
| 90 | .44560 |
| 91 | .44576 |
| 92 | .44592 |
| 93 | .44607 |
| 94 | .44623 |
| 95 | .44638 |
| 96 | .44654 |
| 97 | .44669 |
| 98 | .44685 |
| 99 | .44700 |
| 2800 | 3.44716 |
| 01 | .44731 |
| 02 | .44747 |
| 03 | .44762 |
| 04 | .44778 |
| 05 | .44793 |
| 06 | .44809 |
| 07 | .44824 |
| 08 | .44840 |
| 09 | .44855 |
| 10 | .44871 |
| 11 | .44886 |
| 12 | .44902 |
| 13 | .44917 |
| 14 | .44932 |
| 15 | .44948 |
| 16 | .44963 |
| 17 | .44979 |
| 18 | .44994 |
| 19 | .45010 |
| 20 | .45025 |
| 21 | .45040 |
| 22 | .45056 |
| 23 | .45071 |
| 24 | .45086 |
| 25 | .45102 |
| 26 | .45117 |
| 27 | .45133 |
| 28 | .45148 |
| 29 | .45163 |
| 30 | .45179 |
| 31 | .45194 |
| 32 | .45209 |
| 33 | .45225 |
| 34 | .45240 |
| 35 | .45255 |
| 36 | .45271 |
| 37 | .45287 |
| 38 | .45301 |
| 39 | .45317 |
| 40 | .45332 |
| 41 | .45347 |
| 42 | .45362 |
| 43 | .45378 |
| 44 | .45393 |
| 45 | .45408 |
| 46 | .45423 |
| 47 | .45439 |
| 48 | .45454 |
| 49 | .45469 |
| 50 | .45484 |
| 51 | .45500 |
| 52 | .45515 |
| 53 | .45530 |
| 54 | .45545 [Pg 117] |
| 55 | .45561 |
| 56 | .45576 |
| 57 | .45591 |
| 58 | .45606 |
| 59 | .45621 |
| 60 | .45637 |
| 61 | .45652 |
| 62 | .45667 |
| 63 | .45682 |
| 64 | .45698 |
| 65 | .45712 |
| 66 | .45728 |
| 67 | .45743 |
| 68 | .45758 |
| 69 | .45773 |
| 70 | .45788 |
| 71 | .45803 |
| 72 | .45818 |
| 73 | .45834 |
| 74 | .45849 |
| 75 | .45864 |
| 76 | .45879 |
| 77 | .45894 |
| 78 | .45909 |
| 79 | .45924 |
| 80 | .45939 |
| 81 | .45954 |
| 82 | .45969 |
| 83 | .45984 |
| 84 | .46000 |
| 85 | .46015 |
| 86 | .46030 |
| 87 | .46045 |
| 88 | .46060 |
| 89 | .46075 |
| 90 | .46090 |
| 91 | .46105 |
| 92 | .46120 |
| 93 | .46135 |
| 94 | .46150 |
| 95 | .46165 |
| 96 | .46180 |
| 97 | .46195 |
| 98 | .46210 |
| 99 | .46225 |
| 2900 | 3.46240 |
| 01 | .46255 |
| 02 | .46270 |
| 03 | .46285 |
| 04 | .46300 |
| 05 | .46315 |
| 06 | .46330 |
| 07 | .46344 |
| 08 | .46859 |
| 09 | .46374 |
| 10 | .46389 |
| 11 | .46404 |
| 12 | .46419 |
| 13 | .46434 |
| 14 | .46449 |
| 15 | .46464 |
| 16 | .46479 |
| 17 | .46494 |
| 18 | .46509 |
| 19 | .46523 |
| 20 | .46538 [Pg 118] |
| 21 | .46553 |
| 22 | .46568 |
| 23 | .46583 |
| 24 | .46598 |
| 25 | .46613 |
| 26 | .46627 |
| 27 | .46642 |
| 28 | .46657 |
| 29 | .46672 |
| 30 | .46687 |
| 31 | .46702 |
| 32 | .46716 |
| 33 | .46731 |
| 34 | .46746 |
| 35 | .46761 |
| 36 | .46776 |
| 37 | .46790 |
| 38 | .46805 |
| 39 | .46820 |
| 40 | .46835 |
| 41 | .46849 |
| 42 | .46864 |
| 43 | .46879 |
| 44 | .46894 |
| 45 | .46909 |
| 46 | .46923 |
| 47 | .46938 |
| 48 | .46953 |
| 49 | .46967 |
| 50 | .46982 |
| 51 | .46997 |
| 52 | .47012 |
| 53 | .47026 |
| 54 | .47041 |
| 55 | .47056 |
| 56 | .47070 |
| 57 | .47085 |
| 58 | .47100 |
| 59 | .47114 |
| 60 | .47129 |
| 61 | .47144 |
| 62 | .47159 |
| 63 | .47176 |
| 64 | .47188 |
| 65 | .47202 |
| 66 | .47217 |
| 67 | .47232 |
| 68 | .47246 |
| 69 | .47261 |
| 70 | .47276 |
| 71 | .47290 |
| 72 | .47305 |
| 73 | .47319 |
| 74 | .47334 |
| 75 | .47349 |
| 76 | .47363 |
| 77 | .47378 |
| 78 | .47392 |
| 79 | .47407 |
| 80 | .47422 |
| 81 | .47436 |
| 82 | .47451 |
| 83 | .47465 |
| 84 | .47480 |
| 85 | .47494 |
| 86 | .47509 [Pg 119] |
| 87 | .47524 |
| 88 | .47538 |
| 89 | .47553 |
| 90 | .47567 |
| 91 | .47582 |
| 92 | .47596 |
| 93 | .47611 |
| 94 | .47625 |
| 95 | .47640 |
| 96 | .47654 |
| 97 | .47669 |
| 98 | .47683 |
| 99 | .47698 |
| 3000 | 3.47712 |
| 01 | .47727 |
| 03 | .47741 |
| 03 | .47755 |
| 04 | .47770 |
| 05 | .47784 |
| 06 | .47799 |
| 07 | .47813 |
| 08 | .47828 |
| 09 | .47842 |
| 10 | .47857 |
| 11 | .47871 |
| 12 | .47886 |
| 13 | .47900 |
| 14 | .47914 |
| 15 | .47929 |
| 16 | .47943 |
| 17 | .47958 |
| 18 | .47972 |
| 19 | .47986 |
| 20 | .48001 |
| 21 | .48015 |
| 22 | .48030 |
| 23 | .48044 |
| 24 | .48058 |
| 25 | .48073 |
| 26 | .48087 |
| 27 | .48101 |
| 28 | .48116 |
| 29 | .48130 |
| 30 | .48144 |
| 31 | .48159 |
| 32 | .48173 |
| 33 | .48187 |
| 34 | .48202 |
| 35 | .48216 |
| 36 | .48230 |
| 37 | .48244 |
| 38 | .48259 |
| 39 | .48273 |
| 40 | .48287 |
| 41 | .48302 |
| 42 | .48316 |
| 43 | .48330 |
| 44 | .48344 |
| 45 | .48359 |
| 46 | .48373 |
| 47 | .48387 |
| 48 | .48402 |
| 49 | .48416 |
| 50 | .48430 |
| 51 | .48444 |
| 52 | .48458 [Pg 120] |
| 53 | .48473 |
| 54 | .48487 |
| 55 | .48501 |
| 56 | .48515 |
| 57 | .48530 |
| 58 | .48544 |
| 59 | .48558 |
| 60 | .48572 |
| 61 | .48586 |
| 62 | .48601 |
| 63 | .48615 |
| 64 | .48629 |
| 65 | .48643 |
| 66 | .48657 |
| 67 | .48671 |
| 68 | .48686 |
| 69 | .48700 |
| 70 | .48714 |
| 71 | .48728 |
| 72 | .48742 |
| 73 | .48756 |
| 74 | .48770 |
| 75 | .48785 |
| 76 | .48799 |
| 77 | .48813 |
| 78 | .48827 |
| 79 | .48841 |
| 80 | .48855 |
| 81 | .48869 |
| 82 | .48883 |
| 83 | .48897 |
| 84 | .48911 |
| 85 | .48926 |
| 86 | .48940 |
| 87 | .48954 |
| 88 | .48968 |
| 89 | .48982 |
| 90 | .48996 |
| 91 | .49010 |
| 92 | .49024 |
| 93 | .49038 |
| 94 | .49052 |
| 95 | .49066 |
| 96 | .49080 |
| 97 | .49094 |
| 98 | .49108 |
| 99 | .49122 |
| 3100 | .49136 |
[Pg 121]
This is from Radau’s table. The formula for calculation of difference of altitude of two stations is
in which D is the difference of height in meters, h and h' are barometer readings in millimeters and t and t' are the temperatures in centigrade degrees.
| Mill. | Meters. |
| 500 | 3365.4 |
| 501 | 3349.4 |
| 502 | 3333.5 |
| 503 | 3317.6 |
| 504 | 3301.7 |
| 505 | 3285.9 |
| 506 | 3270.1 |
| 507 | 3254.3 |
| 508 | 3238.5 |
| 509 | 3222.8 |
| 510 | 3207.1 |
| 511 | 3191.5 |
| 512 | 3175.9 |
| 513 | 3160.3 |
| 514 | 3144.7 |
| 515 | 3129.2 |
| 516 | 3113.7 |
| 517 | 3098.2 |
| 518 | 3082.8 |
| 519 | 3067.4 |
| 520 | 3052.0 |
| 521 | 3036.6 |
| 522 | 3021.3 |
| 523 | 3006.0 |
| 524 | 2990.7 |
| 525 | 2975.5 |
| 526 | 2960.3 |
| 527 | 2945.1 |
| 528 | 2930.0 |
| 529 | 2914.9 |
| 530 | 2899.8 |
| 531 | 2884.7 |
| 532 | 2869.7 |
| 533 | 2854.7 |
| 534 | 2839.7 |
| 535 | 2824.7 |
| 536 | 2809.8 |
| 537 | 2794.9 |
| 538 | 2780.0 |
| 539 | 2765.2 |
| 540 | 2750.4 |
| 541 | 2735.6 |
| 542 | 2720.9 |
| 543 | 2706.1 |
| 544 | 2691.4 |
| 545 | 2676.8 |
| 546 | 2662.1 |
| 547 | 2647.5 |
| 548 | 2632.9 |
| 549 | 2618.3 |
| 550 | 2603.8 |
| 551 | 2589.3 |
| 552 | 2574.8 |
| 553 | 2560.3 |
| 554 | 2545.9 |
| 555 | 2531.5 [Pg 122] |
| 556 | 2517.1 |
| 557 | 2502.7 |
| 558 | 2488.4 |
| 559 | 2474.1 |
| 560 | 2459.8 |
| 561 | 2445.6 |
| 562 | 2431.4 |
| 563 | 2417.2 |
| 564 | 2403.0 |
| 565 | 2388.8 |
| 566 | 2374.7 |
| 567 | 2360.6 |
| 568 | 2346.5 |
| 569 | 2332.5 |
| 570 | 2318.4 |
| 571 | 2304.4 |
| 572 | 2290.4 |
| 573 | 2276.5 |
| 574 | 2262.6 |
| 575 | 2248.7 |
| 576 | 2234.8 |
| 577 | 2220.9 |
| 578 | 2207.1 |
| 579 | 2193.3 |
| 580 | 2179.5 |
| 581 | 2165.7 |
| 582 | 2152.0 |
| 583 | 2138.3 |
| 584 | 2124.6 |
| 585 | 2110.9 |
| 586 | 2097.3 |
| 587 | 2083.7 |
| 588 | 2070.1 |
| 589 | 2056.5 |
| 590 | 2042.9 |
| 591 | 2029.4 |
| 592 | 2015.9 |
| 593 | 2002.4 |
| 594 | 1989.0 |
| 595 | 1975.5 |
| 596 | 1962.1 |
| 597 | 1948.7 |
| 598 | 1935.4 |
| 599 | 1922.0 |
| 600 | 1908.7 |
| 601 | 1895.4 |
| 602 | 1882.1 |
| 603 | 1868.8 |
| 604 | 1855.6 |
| 605 | 1842.4 |
| 606 | 1829.2 |
| 607 | 1816.0 |
| 608 | 1802.9 |
| 609 | 1789.8 |
| 610 | 1776.7 |
| 611 | 1763.6 |
| 612 | 1750.5 |
| 613 | 1737.5 |
| 614 | 1724.4 |
| 615 | 1711.4 |
| 616 | 1698.5 |
| 617 | 1685.5 |
| 618 | 1672.6 |
| 619 | 1659.7 |
| 620 | 1646.8 |
| 621 | 1633.9 |
| 622 | 1621.0 |
| 623 | 1608.2 |
| 624 | 1595.4 |
| 625 | 1582.6 |
| 626 | 1569.8 |
| 627 | 1557.1 |
| 628 | 1544.4 |
| 629 | 1531.7 |
| 630 | 1519.0 |
| 631 | 1506.3 |
| 632 | 1493.7 |
| 633 | 1481.0 |
| 634 | 1468.4 |
| 635 | 1455.8 |
| 636 | 1443.3 |
| 637 | 1430.7 |
| 638 | 1418.2 |
| 639 | 1405.7 |
| 640 | 1393.2 |
| 641 | 1380.7 |
| 642 | 1368.3 |
| 643 | 1355.8 |
| 644 | 1343.4 |
| 645 | 1331.0 |
| 646 | 1318.7 |
| 647 | 1306.3 |
| 648 | 1294.0 |
| 649 | 1281.7 |
| 650 | 1269.4 |
| 651 | 1257.1 |
| 652 | 1244.8 |
| 653 | 1232.6 |
| 654 | 1220.4 |
| 655 | 1208.2 |
| 656 | 1196.0 |
| 657 | 1183.8 [Pg 123] |
| 658 | 1171.7 |
| 659 | 1159.5 |
| 660 | 1147.4 |
| 661 | 1135.3 |
| 662 | 1123.3 |
| 663 | 1111.3 |
| 664 | 1099.2 |
| 665 | 1087.2 |
| 666 | 1075.2 |
| 667 | 1063.2 |
| 668 | 1051.2 |
| 669 | 1039.3 |
| 670 | 1027.3 |
| 671 | 1015.4 |
| 672 | 1003.5 |
| 673 | 991.7 |
| 674 | 979.8 |
| 675 | 968.0 |
| 676 | 956.1 |
| 677 | 944.3 |
| 678 | 932.6 |
| 679 | 920.8 |
| 680 | 909.0 |
| 681 | 897.3 |
| 682 | 885.6 |
| 683 | 873.9 |
| 684 | 862.2 |
| 685 | 850.5 |
| 686 | 838.9 |
| 687 | 827.3 |
| 688 | 815.6 |
| 689 | 804.0 |
| 690 | 792.5 |
| 691 | 780.9 |
| 692 | 769.3 |
| 693 | 757.8 |
| 694 | 746.3 |
| 695 | 734.8 |
| 696 | 723.3 |
| 697 | 711.9 |
| 698 | 700.4 |
| 699 | 689.0 |
| 700 | 677.6 |
| 701 | 666.2 |
| 702 | 654.8 |
| 703 | 643.4 |
| 704 | 632.1 |
| 705 | 620.7 |
| 706 | 609.4 |
| 707 | 598.1 |
| 708 | 586.8 |
| 709 | 575.6 |
| 710 | 564.3 |
| 711 | 553.1 |
| 712 | 541 8 |
| 713 | 530.6 |
| 714 | 519.5 |
| 715 | 508.3 |
| 716 | 497.1 |
| 717 | 486.0 |
| 718 | 474.8 |
| 719 | 463.7 |
| 720 | 452.6 |
| 721 | 441.6 |
| 722 | 430.5 |
| 723 | 419.4 |
| 724 | 408.4 |
| 725 | 397.4 |
| 726 | 386.4 |
| 727 | 375.4 |
| 728 | 364.4 |
| 729 | 353.5 |
| 730 | 342.5 |
| 731 | 331.6 |
| 732 | 320.7 |
| 733 | 309.8 |
| 734 | 298.9 |
| 735 | 288.0 |
| 736 | 277.2 |
| 737 | 266.3 |
| 738 | 255.5 |
| 739 | 244.7 |
| 740 | 233.9 |
| 741 | 223.1 |
| 742 | 212.3 |
| 743 | 201.6 |
| 744 | 190.8 |
| 745 | 180.1 |
| 746 | 169.4 |
| 747 | 158.7 |
| 748 | 148.0 |
| 749 | 137.4 |
| 750 | 126.7 |
| 751 | 116.1 |
| 752 | 105.5 |
| 753 | 94.9 |
| 754 | 84.3 |
| 755 | 73.7 |
| 756 | 63.1 |
| 757 | 52.6 |
| 758 | 42.0 |
| 759 | 31.5 [Pg 124] |
| 760 | 21.0 |
| 761 | 10.5 |
| 762 | 0.0 |
| 763 | -10.5 |
| 764 | -20.9 |
| 765 | -31.4 |
| 766 | -41.8 |
| 767 | -52.2 |
| 768 | -62.6 |
| 769 | -73.0 |
| 770 | -83.4 |
| 771 | -93.7 |
| 772 | -104.1 |
| 773 | -114.4 |
| 774 | -124.7 |
| 775 | -135.0 |
| 776 | -145.3 |
| 777 | -155.6 |
| 778 | -165.9 |
| 779 | -176.1 |
| 780 | -186.4 |
[Pg 125]
In comparing the Aneroid with a Mercurial Barometer, correct the latter by the following table, subtracting the corrections.
Brass scale to barometer correct at 62° Fahr.
| Temp. °F. |
30” | 25” | 20” |
|---|---|---|---|
| 32 | .009 | .008 | .006 |
| 35 | .017 | .015 | .012 |
| 40 | .031 | .026 | .021 |
| 45 | .044 | .037 | .030 |
| 50 | .058 | .048 | .038 |
| 55 | .071 | .059 | .047 |
| 60 | .084 | .070 | .056 |
| 65 | .098 | .082 | .065 |
| 70 | .111 | .093 | .074 |
| 75 | .125 | .104 | .083 |
| 80 | .138 | .115 | .092 |
| 85 | .151 | .126 | .101 |
| 90 | .164 | .137 | .110 |
| 95 | .178 | .148 | .118 |
| 100 | .191 | .159 | .127 |
[Pg 126]
| Whole Deg. | Tenths of each Degree. | ||||
|---|---|---|---|---|---|
| .0 | .2 | .4 | .6 | .8 | |
| in. | in. | in. | in. | in. | |
| 183 | 16.317 | 16.389 | 16.461 | 16.533 | 16.605 |
| 184 | 16.618 | 16.752 | 16.826 | 16.900 | 16.974 |
| 185 | 17.048 | 17.122 | 17.197 | 17.272 | 17.348 |
| 186 | 17.423 | 17.499 | 17.575 | 17.652 | 17.729 |
| 187 | 17.806 | 17.883 | 17.961 | 18.039 | 18.117 |
| 188 | 18.195 | 18.274 | 18.353 | 18.432 | 18.512 |
| 189 | 18.592 | 18.672 | 18.753 | 18.833 | 18.914 |
| 190 | 18.996 | 19.077 | 19.159 | 19.241 | 19.324 |
| 191 | 19.407 | 19.490 | 19.573 | 19.657 | 19.741 |
| 192 | 19.825 | 19.910 | 19.995 | 20.080 | 20.166 |
| 193 | 20.251 | 20.338 | 20.424 | 20.511 | 20.598 |
| 194 | 20.685 | 20.773 | 20.861 | 20.949 | 21.038 |
| 195 | 21.126 | 21.216 | 21.305 | 21.395 | 21.485 |
| 196 | 21.576 | 21.666 | 21.758 | 21.849 | 21.941 |
| 197 | 22.033 | 22.125 | 22.218 | 22.311 | 22.404 |
| 198 | 22.498 | 22.592 | 22.686 | 22.781 | 22.876 |
| 199 | 22.971 | 23.067 | 23.163 | 23.259 | 23.356 |
| 200 | 23.453 | 23.550 | 23.648 | 23.746 | 23.845 |
| 201 | 23.943 | 24.042 | 24.142 | 24.241 | 24.341 |
| 202 | 24.442 | 24.542 | 24.644 | 24.745 | 24.847 |
| 203 | 24.949 | 25.051 | 25.154 | 25.257 | 25.361 |
| 204 | 25.465 | 25.569 | 25.674 | 25.779 | 25.884 |
| 205 | 25.990 | 26.096 | 26.202 | 26.309 | 26.416 |
| 206 | 26.523 | 26.631 | 26.740 | 26.848 | 26.957 |
| 207 | 27.066 | 27.176 | 27.286 | 27.397 | 27.507 |
| 208 | 27.618 | 27.730 | 27.842 | 27.954 | 28.067 |
| 209 | 28.180 | 28.293 | 28.407 | 28.521 | 28.636 |
| 210 | 28.751 | 28.866 | 28.982 | 29.098 | 29.215 |
| 211 | 29.331 | 29.449 | 29.566 | 29.684 | 29.803 |
| 212 | 29.922 | 30.041 | 30.161 | 30.281 | 30.401 |
Transcriber’s Notes:
The cover image was created by the transcriber, and is in the public domain.
The illustrations have been moved so that they do not break up paragraphs and so that they are next to the text they illustrate.
Typographical and punctuation errors have been silently corrected.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org. If you are not located in the United States, you will have to check the laws of the country where you are located before using this eBook.